题目内容
如图,在四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB,平面SAD⊥平面ABCD,M是线段AD上一点,AM=AB,DM=DC,SM⊥AD。
(1)证明:BM⊥平面SMC;
(2)设三棱锥C-SBM与四棱锥S-ABCD的体积分别为V1与V,求 的值.
的值.
(1)证明:BM⊥平面SMC;
(2)设三棱锥C-SBM与四棱锥S-ABCD的体积分别为V1与V,求
 的值.
的值. 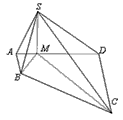
(1)证明:∵平面SAD⊥平面ABCD,平面SAD∩平面ABCD=AD, SM 平面SAD,SM⊥AD,
平面SAD,SM⊥AD,
∴SM⊥平面ABCD,
∵BM 平面ABCD,
平面ABCD,
∴SM⊥BM,
∵四边形ABCD是直角梯形,AB∥CD,AM=AB,DM=DC,
∴△MAB,△MDC都是等腰直角三角形,
∴∠AMN=∠CMF=45°,∠BMC=90°,BM⊥CM,
∵SM 平面SMC,CM
平面SMC,CM 平面SMC,SM∩CM=M,
平面SMC,SM∩CM=M,
∴BM⊥平面SMC。
(2) 解: 三棱锥C-SBM与三棱锥S-CBM的体积相等,
由(1) 知SM⊥平面ABCD,得 ,
,
设AB=a,由CD=3AB,AM=AB,DM=DC,
得
从而 。
。
 平面SAD,SM⊥AD,
平面SAD,SM⊥AD,∴SM⊥平面ABCD,
∵BM
 平面ABCD,
平面ABCD, ∴SM⊥BM,
∵四边形ABCD是直角梯形,AB∥CD,AM=AB,DM=DC,
∴△MAB,△MDC都是等腰直角三角形,
∴∠AMN=∠CMF=45°,∠BMC=90°,BM⊥CM,
∵SM
 平面SMC,CM
平面SMC,CM 平面SMC,SM∩CM=M,
平面SMC,SM∩CM=M,∴BM⊥平面SMC。
(2) 解: 三棱锥C-SBM与三棱锥S-CBM的体积相等,
由(1) 知SM⊥平面ABCD,得
 ,
,设AB=a,由CD=3AB,AM=AB,DM=DC,
得

从而
 。
。
练习册系列答案
相关题目
 如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE=
如图,在四棱锥S-ABCD中,AD∥BC且AD⊥CD;平面CSD⊥平面ABCD,CS⊥DS,CS=2AD=2;E为BS的中点,CE= 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点 如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=
如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,SA=AB=AD= 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F分别为AB,SC的中点. 如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.底面ABCD为矩形,
如图,在四棱锥S-ABCD中,平面SAD⊥平面ABCD.底面ABCD为矩形,