题目内容
已知直线AB与抛物线y2=2px(p>0)交于两点A(x1,y1),B(x2,y2),且y1y2=-p2. 求证:直线AB经过抛物线的焦点.
分析:设直线AB的方程为:y=kx+b,由
,得k2x2+(2bk-2p)x+b2=0,由A(x1,y1),B(x2,y2),知x1•x2=
,由y2=2px(p>0),y1y2=-p2,知x1x2 =
•
=
=
,由此能够证明直线AB经过抛物线的焦点.
|
| b2 |
| k2 |
| y12 |
| 2p |
| y22 |
| 2p |
| p4 |
| 4p2 |
| b2 |
| k2 |
解答:证明:设直线AB的方程为:y=kx+b,
由
,得(kx+b)2=2px,
整理,得k2x2+(2bk-2p)x+b2=0,
∵A(x1,y1),B(x2,y2),
∴x1•x2=
,
∵y2=2px(p>0),y1y2=-p2,
∴x1x2 =
•
=
=
,
∴k=
,或k=-
,
∴y=
x+b(舍)或y=-
x+b,
当y=0时,x=
.
故直线AB经过抛物线的焦点F(
,0).
由
|
整理,得k2x2+(2bk-2p)x+b2=0,
∵A(x1,y1),B(x2,y2),
∴x1•x2=
| b2 |
| k2 |
∵y2=2px(p>0),y1y2=-p2,
∴x1x2 =
| y12 |
| 2p |
| y22 |
| 2p |
| p4 |
| 4p2 |
| b2 |
| k2 |
∴k=
| 2b |
| p |
| 2b |
| p |
∴y=
| 2b |
| p |
| 2b |
| p |
当y=0时,x=
| p |
| 2 |
故直线AB经过抛物线的焦点F(
| p |
| 2 |
点评:本题考查抛物线的性质和应用,是中档题.解题时要认真审题,注意直线和抛物线位置关系的应用,合理地运用韦达定理进行求解.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
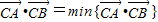 ,则下列一定成立的是( )
,则下列一定成立的是( )