题目内容
已知直线AB与抛物线y2=4x交于A，B两点，M为AB的中点，C为抛物线上一个动点，若C0满足
•
=min{
•
}，则下列一定成立的是（ ）
| C0A |
| C0B |
| CA |
| CB |
分析：先利用向量加减法的几何意义化简
•
，从而得出
•
=|
|2-|
|2，故有min{
•
}=|
|min，l是抛物线过C0的切线，结合抛物线的性质即可得出答案．
| CA |
| CB |
| CA |
| CB |
| CM |
| AM |
| CA |
| CB |
| CM |
解答：
解：∵
•
=（
-
）•（
-
）
=|
|2-
•(
+
)+
•
=|
|2-|
|2，
∴min{
•
}=|
|min，
∴CM⊥l．其中l是抛物线过C0的切线．
故选B．
解：∵| CA |
| CB |
=（
| CM |
| AM |
| CM |
| BM |
=|
| CM |
| CM |
| AM |
| BM |
| AM |
| BM |
=|
| CM |
| AM |
∴min{
| CA |
| CB |
| CM |
∴CM⊥l．其中l是抛物线过C0的切线．
故选B．
点评：本题主要考查了平面向量的加减运算，平面向量数量积的运算，抛物线的方程，考查了转化思想，属于难题．
练习册系列答案
教学练新同步练习系列答案
课前课后同步练习系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
相关题目
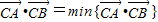，则下列一定成立的是（ ）