题目内容
设P,Q为△ABC内的两点,且
|
分析:设P到边AB的距离为h1,Q到边AB的距离为h2,则△ABP的面积与△ABQ的面积之比为
,h1是向量AP与AB边上的单位法向量
的乘积的绝对值,h2是向量AQ与AB边上的单位法向量
的乘积的绝对值.
| h1 |
| h2 |
| e |
| e |
解答:解:设P到边AB的距离为h1,Q到边AB的距离为h2,则△ABP的面积与△ABQ的面积之比为
,
设AB边上的单位法向量为
,
•
=0,
则h1=|
•
|=|(m
+n
)•
|=|m•
•
+n
•
|=|n
•
|,
同理可得h2=|q
•
|,
∴
=|
|=
,
故答案为 n:q.
| h1 |
| h2 |
设AB边上的单位法向量为
| e |
| AB |
| e |
则h1=|
| AP |
| e |
| AB |
| AC |
| e |
| AB |
| e |
| AC |
| e |
| AC |
| e |
同理可得h2=|q
| AC |
| e |
∴
| h1 |
| h2 |
| n |
| q |
| n |
| q |
故答案为 n:q.
点评:本题考查向量共线定理、向量数量积的意义,体现了转化的数学思想.

练习册系列答案
相关题目
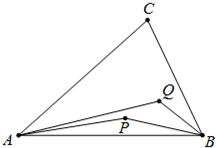 如图,设P,Q为△ABC内的两点,且
如图,设P,Q为△ABC内的两点,且 如图,设P,Q为△ABC内的两点,且
如图,设P,Q为△ABC内的两点,且