题目内容
1.已知函数f(x)是定义在R上的偶函数,且当x≤0时f(x)=x2+4x.(I)求f(-1),f(f(1))的值;
(Ⅱ)求函数f(x)的解析式;
(Ⅲ)画出函数f(x)的大致图象,并求出函数的值域.
分析 (I)根据函数f(x)的解析式,求得f(-1),f(f(1))的值.
(Ⅱ)由条件求得x>0时的解析式,即可得到函数f(x)的解析式.
(Ⅲ)根据函数的解析式,画出函数f(x)的大致图象,从而求出函数的值域.
解答 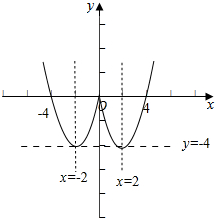 解:(I)由于函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+4x.
解:(I)由于函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)=x2+4x.
故f(-1)=1-4=-3,f(f(1))=f(-3)=9-12=-3.
(Ⅱ)设x>0,则-x<0,f(-x)=(-x)2+4(-x)=x2-4x=f(x),
∴f(x)=x2-4x;
综上可得,函数f(x)=$\left\{\begin{array}{l}{{x}^{2}+4x,x≤0}\\{{x}^{2}-4x,x<0}\end{array}\right.$.
(Ⅲ)画出函数f(x)的大致图象,如图所示:
故函数的值域为[-4,+∞).
点评 本题主要考查求函数的解析式,求函数的值及函数的值域,函数的图象,属于中档题.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
11.底面为菱形的直棱柱ABCD-A1B1C1D1的两个对角面ACC1A1和BDD1B1的面积为6和8,则该棱柱的侧面积为( )
| A. | 18 | B. | 20 | C. | 36 | D. | 40 |
12.设关于x、y的不等式组$\left\{\begin{array}{l}{x+y-1≥0}\\{x-1≤0}\\{ax-y+1≥0}\end{array}\right.$表示的平面区域内存在点P(x0,y0),满足2x0+y0=4,则a的取值范围是( )
| A. | (-∞,-2)∪[1,+∞) | B. | (-∞,-2) | C. | (-2,1] | D. | [1,+∞) |
6.不等式-25x2+10x-1≥0的解集为( )
| A. | ∅ | B. | $\left\{{x\left|{x=\frac{1}{5}}\right.}\right\}$ | C. | $\left\{{x\left|{x≠\frac{1}{5}}\right.}\right\}$ | D. | $\left\{{x\left|{x≤\frac{1}{5}}\right.}\right\}$ |
11.已知点M是焦点为F的抛物线y2=8x上一动点,当△MOF的面积是$\sqrt{3}$时,线段MF的长为( )
| A. | $\frac{3}{8}$ | B. | $\frac{11}{8}$ | C. | $\frac{17}{8}$ | D. | $\frac{19}{8}$ |