题目内容
3．函数f（x）=lnx-x2的图象大致是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 求导f′（x）=$\frac{1}{x}$-2x=$\frac{（1+\sqrt{2}x）（1-\sqrt{2}x）}{x}$，从而判断函数的单调性与最值，从而确定答案．
解答 解：∵f（x）=lnx-x2，
∴f′（x）=$\frac{1}{x}$-2x=$\frac{（1+\sqrt{2}x）（1-\sqrt{2}x）}{x}$，
∴f（x）在（0，$\frac{\sqrt{2}}{2}$）上是增函数，在（$\frac{\sqrt{2}}{2}$，+∞）上是减函数，
且f（$\frac{\sqrt{2}}{2}$）=ln$\frac{\sqrt{2}}{2}$-$\frac{1}{2}$＜0，
故选：A．
点评 本题考查了导数的综合应用及函数的性质的判断与应用．
练习册系列答案
相关题目
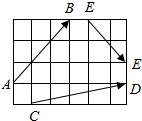图中，小正方形的边长为1，则|$\overrightarrow{AB}$|=$3\sqrt{2}$，|$\overrightarrow{CD}$|=$\sqrt{26}$，|$\overrightarrow{EF}$|=$2\sqrt{2}$．