题目内容
已知 ,其中ω>0.设函数
,其中ω>0.设函数 ,且函数f(x)的周期为π.
,且函数f(x)的周期为π.(I)求ω的值;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,且a,b,c成等差:当f(B)=1'时,判断△ABC的形状.
【答案】分析:(I)根据向量积得出f(x)=cos2ωx+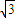 sin2ωx进而化简成f(x)=2sin(2ωx+
sin2ωx进而化简成f(x)=2sin(2ωx+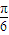 ),然后根据周期公式得出答案.
),然后根据周期公式得出答案.
(II) 首先根据条件求出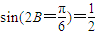 ,进而由角的范围求出B的度数,再由等差数列的性质得出2b=a+c,从而利用余弦定理求出角B的度数进而判断三角形的形状.
,进而由角的范围求出B的度数,再由等差数列的性质得出2b=a+c,从而利用余弦定理求出角B的度数进而判断三角形的形状.
解答:解:
(I)∵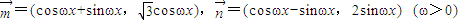

∵函数f(x)的周期为π∴T=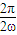 =π∴ω=1
=π∴ω=1
(Ⅱ)在△ABC中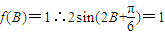 ∴
∴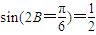
又∵0<B<π∴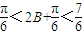 π
π
∵2B+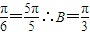 ∵a,b,c成等差∴2b=a+c
∵a,b,c成等差∴2b=a+c
∴cosB=cos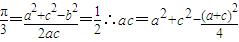
化简得:a=c又∵B=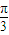 ∴△ABC为正三角形
∴△ABC为正三角形
点评:本题考查了三角函数周期性的求法以及利用余弦定理判断三角形的形状,解题过程要特别注意角的范围,属于中档题.
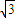 sin2ωx进而化简成f(x)=2sin(2ωx+
sin2ωx进而化简成f(x)=2sin(2ωx+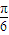 ),然后根据周期公式得出答案.
),然后根据周期公式得出答案.(II) 首先根据条件求出
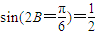 ,进而由角的范围求出B的度数,再由等差数列的性质得出2b=a+c,从而利用余弦定理求出角B的度数进而判断三角形的形状.
,进而由角的范围求出B的度数,再由等差数列的性质得出2b=a+c,从而利用余弦定理求出角B的度数进而判断三角形的形状.解答:解:
(I)∵
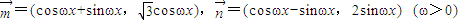

∵函数f(x)的周期为π∴T=
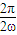 =π∴ω=1
=π∴ω=1(Ⅱ)在△ABC中
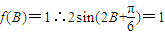 ∴
∴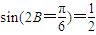
又∵0<B<π∴
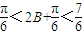 π
π∵2B+
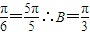 ∵a,b,c成等差∴2b=a+c
∵a,b,c成等差∴2b=a+c∴cosB=cos
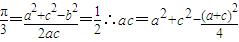
化简得:a=c又∵B=
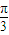 ∴△ABC为正三角形
∴△ABC为正三角形点评:本题考查了三角函数周期性的求法以及利用余弦定理判断三角形的形状,解题过程要特别注意角的范围,属于中档题.

练习册系列答案
相关题目
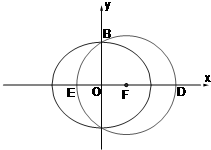 如图,已知F(c,0)是椭圆
如图,已知F(c,0)是椭圆 其中a>0.
其中a>0.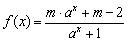 (其中a>0且a≠1,m∈R)是定义在R上的奇函数.记
(其中a>0且a≠1,m∈R)是定义在R上的奇函数.记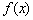 的反函数为
的反函数为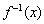 .
.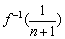 (n∈N*),它的前n项和为Sn,求使不等式Sn<
(n∈N*),它的前n项和为Sn,求使不等式Sn<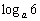 成立的n的取值.
成立的n的取值.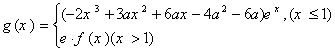 (e是自然对数的底数),是否存在a,使
(e是自然对数的底数),是否存在a,使