Question

 

已知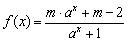（其中a>0且a≠1，m∈R）是定义在R上的奇函数．记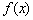的反函数为．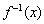

（1）求实数m的值及；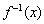

（2）设数列{a_n}满足a_n=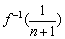（n∈N*），它的前n项和为S_n，求使不等式S_n<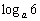成立的n的取值．

 

 

 

 

 

 

Answer 1

【答案】

 解：（1）f (x)是定义在R上的奇函数，

∴  f (0)=0，即，解得m=1．  ………………………………2分

∴   (x∈R)．

令，反解得，

∴ （-1<x<1）．  ……………………………………………6分

（2）由已知有a_n==（n∈N*），

∴ S_n=+++…+

       =

       =． ………………………………………………………9分

于是由题得<，

 ∴ 当a>1时，<6，解得-5<n<2．

当0<a<1时，>6，解得n<-5，或n>2．

 ∵ n∈N*，

∴ 当a>1时，n=1；当0<a<1时，n取大于2的所有整数． …………12分