题目内容
已知函数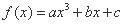 在
在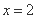 处取得极值为
处取得极值为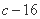
(1)求a、b的值;
(2)若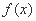 有极大值28,求
有极大值28,求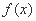 在
在 上的最大值和最小值.
上的最大值和最小值.
解析:(1)因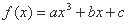 故
故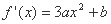
由于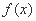 在点
在点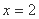 处取得极值
处取得极值
故有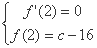 即
即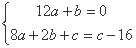 ,
,
化简得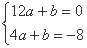 解得
解得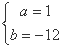 4分
4分
(2)由(1)知 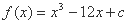 ,
,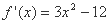
令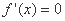 ,得
,得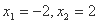 当
当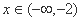 时,
时,
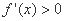 故
故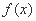 在
在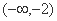 上为增函数;
上为增函数;
当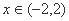 时,
时,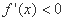 ,故
,故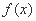 在
在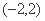 上为减函数
上为减函数
当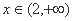 时
时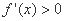 ,故
,故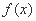 在
在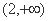 上为增函数。 8分
上为增函数。 8分
由此可知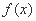 在
在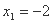 处取得极大值
处取得极大值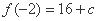 ,
,
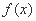 在
在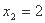 处取得极小值
处取得极小值
由题设条件知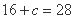 得
得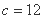 10分
10分
此时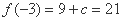 ,
,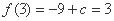 ,
,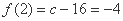
因此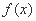 上
上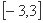 的最小值为
的最小值为 ,最大值为
,最大值为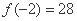 12分
12分

练习册系列答案
相关题目
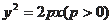 与双曲线
与双曲线 有相同的焦点F,点A是两曲线的交点,且
有相同的焦点F,点A是两曲线的交点,且 轴,则双曲线的离心率为 ( )
轴,则双曲线的离心率为 ( )  B.
B.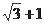 C.
C. D.
D.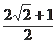
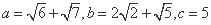 则
则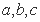 的大小关系为
的大小关系为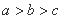 B.
B.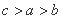 C.
C.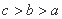 D.
D.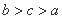
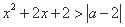 对于一切实数
对于一切实数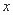 均成立,则实数
均成立,则实数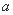 的取值范围是______.
的取值范围是______.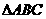 中,
中,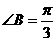 ,三边长a,b,c成等差数列,且
,三边长a,b,c成等差数列,且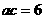 ,则b的值是
,则b的值是 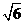 B.
B.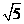 C.
C.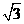 D.
D.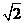
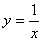 有一切线与直线
有一切线与直线 垂直,则切点可以为( )
垂直,则切点可以为( )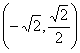 B .
B . 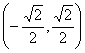 C.
C. 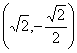 D.
D.