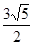题目内容
正方体 中,
中, 为侧面
为侧面 所在平面上的一个动点,且
所在平面上的一个动点,且 到平面
到平面 的距离是
的距离是 到直线
到直线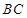 距离的
距离的 倍,则动点
倍,则动点 的轨迹为( )
的轨迹为( )
| A.椭圆 | B.双曲线 | C.抛物线 | D.圆 |
A
解析试题分析:如下图,过点 作
作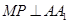 于点
于点 ,连接
,连接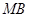 ,因为
,因为 是正方体,故点
是正方体,故点 到平面
到平面 的距离就是
的距离就是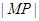 ,而点
,而点 到直线
到直线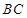 的距离就是
的距离就是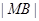 ,所以有
,所以有 .法一:以
.法一:以 为坐标原点,
为坐标原点,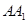 为
为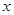 轴,
轴,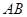 为
为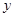 轴,建立平面直角坐标系,不妨设
轴,建立平面直角坐标系,不妨设 ,动点
,动点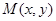 ,则
,则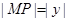 ,
, ,所以
,所以 ,整理可得
,整理可得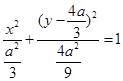 ,由此可知,点
,由此可知,点 的轨迹为椭圆;法二:在得到
的轨迹为椭圆;法二:在得到 时,这说明在平面
时,这说明在平面 上动点
上动点 到定点
到定点 的距离与到定直线
的距离与到定直线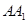 的距离之比为
的距离之比为 ,由圆锥曲线的第二定义可知,该动点
,由圆锥曲线的第二定义可知,该动点 的轨迹为椭圆,可得答案A.
的轨迹为椭圆,可得答案A.
考点:1.立体几何中的轨迹问题;2.圆锥曲线的图像与性质.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
已知椭圆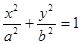
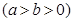 的离心率
的离心率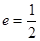 ,右焦点为
,右焦点为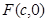 ,方程
,方程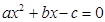 的两个实根
的两个实根 ,
,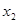 ,则点
,则点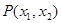 ( )
( )
A.必在圆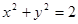 上 上 | B.必在圆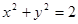 内 内 |
C.必在圆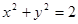 外 外 | D.以上三种情况都有可能 |
已知抛物线 上一点P到y轴的距离为5,则点P到焦点的距离为( )
上一点P到y轴的距离为5,则点P到焦点的距离为( )
| A.5 | B.6 | C.7 | D.8 |
若焦距为 的双曲线的两条渐近线互相垂直,则此双曲线的实轴长为( )
的双曲线的两条渐近线互相垂直,则此双曲线的实轴长为( )
A. | B. | C.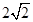 | D.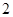 |
设 为抛物线
为抛物线 的焦点,
的焦点, 为抛物线上三点,若
为抛物线上三点,若 为
为 的重心,则
的重心,则 的值为( )
的值为( )
| A.1 | B.2 | C.3 | D.4 |
已知双曲线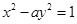 的两条渐近线方程为
的两条渐近线方程为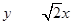 ,那么此双曲线的虚轴长为( )
,那么此双曲线的虚轴长为( )
A.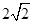 | B.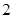 | C.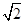 | D. |
若抛物线 的焦点与双曲线
的焦点与双曲线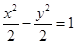 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )
A. | B. | C. | D. |
已知椭圆 的左、右焦点分别为
的左、右焦点分别为 ,若椭圆上存在点P使
,若椭圆上存在点P使 ,则该椭圆的离心率的取值范围为( )
,则该椭圆的离心率的取值范围为( )
A.(0, | B.( ) ) | C.(0, ) ) | D.( ,1) ,1) |
 (a>b>0)的一个焦点和一个顶点得到的直线方程为x-2y+2=0,则该椭圆的离心率为( )
(a>b>0)的一个焦点和一个顶点得到的直线方程为x-2y+2=0,则该椭圆的离心率为( )