题目内容
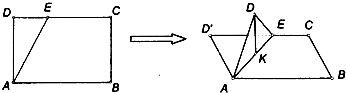
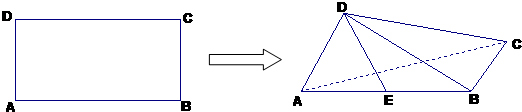
 如图,在长方形ABCD中,AB=2,AD=1,O为AB上的动点,P是线段DO的中点,则(
如图,在长方形ABCD中,AB=2,AD=1,O为AB上的动点,P是线段DO的中点,则(| AO |
| AD |
| AB |
4
4
.分析:根据条件首先设出AO:OB=x,用向量
和
作为基底,把数量积表示为关于
和
的积,进而表示为含x的形式,化简可得(
+
)•
=
,根据x的取值范围可以求出最大值.
| AB |
| AD |
| AB |
| AD |
| AO |
| AD |
| AB |
| 4 |
| 1+x |
解答:解:由题意,设AO:OB=x,(x≥0)
则
=
,故(
+
)=2
=
+
∴(
+
)•
=
|
| 2+
•
∵AB⊥AD⇒
•
=0
∴(
+
)•
=
故当x=0时,(
+
)•
的最大值是4
故答案为4
则
| AO |
| 1 |
| 1+x |
| AB |
| AO |
| AD |
| AP |
| 1 |
| (1+x) |
| AB |
| AD |
∴(
| AO |
| AD |
| AB |
| 1 |
| 1+x |
| AB |
| AB |
| AD |
∵AB⊥AD⇒
| AB |
| AD |
∴(
| AO |
| AD |
| AB |
| 4 |
| 1+x |
故当x=0时,(
| AO |
| AD |
| AB |
故答案为4
点评:本题考查利用向量的运算法则将未知向量用已知的向量表示;将未知向量的数量积用已知向量的数量积表示,从而找到欲求的最大值.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
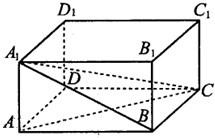 若一个n面体有m个面时直角三角形,则称这个n面体的直度为
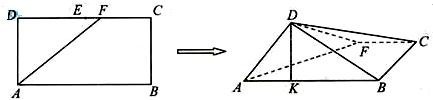
若一个n面体有m个面时直角三角形,则称这个n面体的直度为 如图,在长方形ABCD中,AB=
如图,在长方形ABCD中,AB=