题目内容
9.函数f(x)=x-$\frac{1}{3}$x3的递增区间为( )| A. | (-∞,-1) | B. | (-1,1) | C. | (1,+∞) | D. | (0,+∞) |
分析 先求函数导数,令导数大于等于0,解得x的范围就是函数的单调增区间.
解答 解:对函数y=x-$\frac{1}{3}$x3求导,得,y′=1-x2,
令y′>0,即1-x2>0,解得,-1<x<1
∴函数y=x-$\frac{1}{3}$x3的递增区间为(-1,1),
故选:B.
点评 本题主要考查了导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
19.大衍数列,来源于《乾坤谱》中对易传“大衍之数五十”的推论.主要用于解释中国传统文化中的太极衍生原理.数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和.是中华传统文化中隐藏着的世界数学史上第一道数列题.其前10项依次是0、2、4、8、12、18、24、32、40、50…,则此数列第20项为( )
| A. | 180 | B. | 200 | C. | 128 | D. | 162 |
20.用反证法证明命题:“若a,b∈Z,ab能被5整除,则a,b中至少有一个能被5整除”,那么假设的内容是( )
| A. | a,b都能被5整除 | B. | a,b都不能被5整除 | ||
| C. | a,b有一个能被5整除 | D. | a,b有一个不能被5整除 |
17.与两个相交平面的交线平行的直线和这两个平面的位置关系是( )
| A. | 都平行 | B. | 都相交 | ||
| C. | 在两平面内 | D. | 至少和其中一个平行 |
1.若|$\frac{x}{x+1}$|>$\frac{x}{x+1}$则实数x的取值范围是( )
| A. | (-1,0) | B. | [-1,0] | C. | (-∞,-1)∪(0,+∞) | D. | (-∞,-1]∪[0,+∞) |
18.函数f(x)=$\frac{4}{x^2}$+3x(x>0)取得最小值时,x的值是( )
| A. | $\frac{1}{3}\root{3}{36}$ | B. | $\frac{2}{3}\root{3}{9}$ | C. | $\frac{1}{3}\sqrt{36}$ | D. | $\frac{2}{3}\sqrt{9}$ |
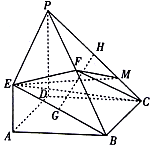 如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.
如图,已知四边形ABCD是正方形,EA⊥平面ABCD,PD∥EA,AD=PD=2EA=2,F,G,H分别为BP,BE,PC的中点.