题目内容
已知圆P与圆x2+y2-2x=0外切于点（1，-1），并且圆心在直线x+y+3=0上，求圆P的方程．
考点：圆的一般方程
专题：直线与圆
分析：根据条件求出圆心坐标和半径即可得到结论．
解答：
解：圆x2+y2-2x=0的标准方程为（x-1）2+y2=1，圆心为C（1，0），半径r=1，
则圆P的横坐标为1，设P（1，b），
∵圆心在直线x+y+3=0上，
∴1+b+3=0，解得b=-4，
即圆心P（1，-4），则圆P的半径R=|-4+1|=3，
则圆的方程为（x-1）2+（y+4）y2=9
则圆P的横坐标为1，设P（1，b），
∵圆心在直线x+y+3=0上，
∴1+b+3=0，解得b=-4，
即圆心P（1，-4），则圆P的半径R=|-4+1|=3，
则圆的方程为（x-1）2+（y+4）y2=9
点评：本题主要考查圆的方程的求解，根据圆与圆的位置关系确定圆心和半径是解决本题的关键．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
下列函数在区间（0，+∞）是增函数的是（ ）
| A、y=tanx |
| B、f（x）=sinx |
| C、y=x2-x+1 |
| D、y=ln（x+1） |
如果函数f（x）=sin2x+acos2x的图象关于点（
，0）成中心对称，那么a=（ ）
| π |
| 8 |
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
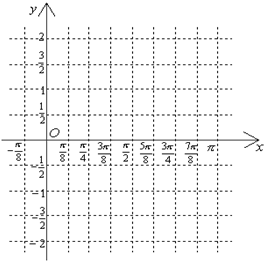已知曲线f（x）=Asin（ωx+ϕ）+B（A＞0，ω＞0，|φ|＜