题目内容
求函数y=-cos2x+
+
的最大值及最小值，并写出x取何值时函数有最大值和最小值．
【答案】分析：先进行配方找出对称轴，而-1≤cosx≤1，利用对称轴与区间的位置关系求出最值及相应的x取值．
解答：解：令t=cosx，则t∈[-1，1]
所以函数解析式可化为：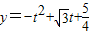
=
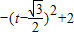
因为t∈[-1，1]，所以由二次函数的图象可知：
当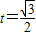
时，函数有最大值为2，此时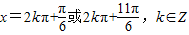
当t=-1时，函数有最小值为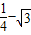
，此时x=2kπ+π，k∈Z
点评：本题以三角函数为载体考查二次函数的值域，属于求二次函数的最值问题，属于基本题．
解答：解：令t=cosx，则t∈[-1，1]
所以函数解析式可化为：
=
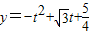
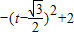
因为t∈[-1，1]，所以由二次函数的图象可知：
当
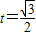时，函数有最大值为2，此时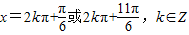当t=-1时，函数有最小值为
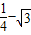，此时x=2kπ+π，k∈Z点评：本题以三角函数为载体考查二次函数的值域，属于求二次函数的最值问题，属于基本题．
练习册系列答案
相关题目