题目内容
12.若f(x)=e-x(cos x+sin x),则f′(x)=-2e-xsinx.分析 根据题意,将f(x)的解析式变形可得f(x)=$\frac{cosx+sinx}{{e}^{x}}$,利用商的导数计算法则计算可得答案.
解答 解:根据题意,f(x)=e-x(cos x+sin x)=$\frac{cosx+sinx}{{e}^{x}}$,
f′(x)=$\frac{(cosx+sinx)′{e}^{x}-(cosx+sinx)•({e}^{x})′}{{e}^{2x}}$=$\frac{-2sinx}{{e}^{x}}$=-2e-xsin x,
答案:-2e-xsin x
点评 本题考查导数的计算,关键是掌握导数的计算公式以及法则.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
20.若等差数列{an}的前7项和S7=77,则a4等于( )
| A. | 11 | B. | 12 | C. | 7 | D. | 不能确定 |
7.用二分法来求方程x2-2=0得到的程序为( )
| A. | 组织结构图 | B. | 工序流程图 | C. | 知识结构图 | D. | 程序流程图 |
2.下列说法正确的是( )
| A. | $\frac{f({x}_{0})-f({x}_{0}+△x)}{△x}$叫做函数y=f(x)在区间[x0,x0+△x](△x>0)的平均变化率 | |
| B. | 导数是一个常数 | |
| C. | 函数y=f(x)的导数f′(x)=$\underset{lim}{△x→0}$$\frac{f(x+△x)-f(x)}{△x}$ | |
| D. | 以上说法都不对 |
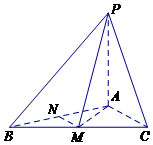 在三棱锥P-ABC中,PA⊥平面ABC,AB=AC=2,BC=2$\sqrt{3}$,M,N分别为BC,AB中点.
在三棱锥P-ABC中,PA⊥平面ABC,AB=AC=2,BC=2$\sqrt{3}$,M,N分别为BC,AB中点.