题目内容
| |||||||||||||||
答案:
解析:
解析:
(1) |
取AB中点G,连结CG、FG ∵F为BE中点 ∴FG∥AE,FG= ∴FG∥CD,FG=CD ∴四边形FGCD为平行四边形 ∴DF∥CG ∴DF∥面ABC |
(2) |
∵△ABC为正三角形 ∴CG⊥AB 又EA⊥平面ABC ∴CG⊥AE. ∴CG⊥平面AEB ∴CG⊥AF 又CG∥DF, ∴AF⊥DF 又AE=AB, ∴AF⊥BE ∴AF⊥平面BED ∴AF⊥BD |
(3) |
取AC中点M,连结BM,易知面AEDC⊥面ABC ∴VABCED=VB-AEDC= |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


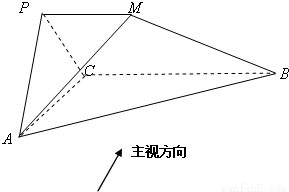
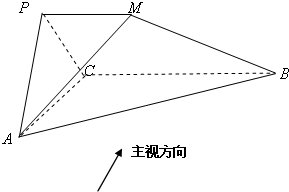 如图所示几何体中,平面PAC⊥平面ABC,PM∥BC,PA=PC,AC=1,BC=2PM=2,AB=
如图所示几何体中,平面PAC⊥平面ABC,PM∥BC,PA=PC,AC=1,BC=2PM=2,AB=
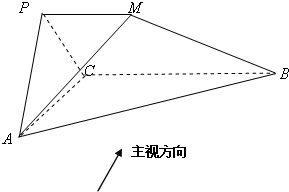 如图所示几何体中,平面PAC⊥平面ABC,PM∥BC,PA=PC,AC=1,BC=2PM=2,AB=
如图所示几何体中,平面PAC⊥平面ABC,PM∥BC,PA=PC,AC=1,BC=2PM=2,AB= ,若该几何体左视图(侧视图)的面积为
,若该几何体左视图(侧视图)的面积为 .
. ,若该几何体左视图(侧视图)的面积为
,若该几何体左视图(侧视图)的面积为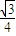 .
.