题目内容
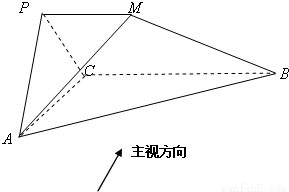
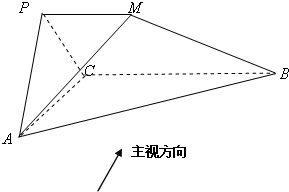
 如图所示几何体中,平面PAC⊥平面ABC,PM∥BC,PA=PC,AC=1,BC=2PM=2,AB=
如图所示几何体中,平面PAC⊥平面ABC,PM∥BC,PA=PC,AC=1,BC=2PM=2,AB=| 5 |
| ||
| 4 |
(1)求证:PA⊥BC;
(2)画出该几何体的主视图(正视图)并求其面积S;
(3)求出多面体PMABC的体积V.
分析:(1)先由勾股定理证明BC与AC垂直,再由面面垂直的性质定理,证明BC与平面PAC垂直,最后由线面垂直的定义证明BC与PA垂直
(2)利用正投影的方法,该几何体的正视图是一个以PM、BC长为上下底边长,以点P到底面ABC的距离为高的直角梯形,由梯形面积公式即可计算其面积
(3)此多面体为一个以四边形PCBM为底面,以点A为顶点的四棱锥,由于底面为直角梯形,高为点A到PC的距离,故利用椎体的体积计算公式即可求得其体积
(2)利用正投影的方法,该几何体的正视图是一个以PM、BC长为上下底边长,以点P到底面ABC的距离为高的直角梯形,由梯形面积公式即可计算其面积
(3)此多面体为一个以四边形PCBM为底面,以点A为顶点的四棱锥,由于底面为直角梯形,高为点A到PC的距离,故利用椎体的体积计算公式即可求得其体积
解答:解:(1)∵AC=1,BC=2,AB=
,
∴AC2+BC2=AB2,∴AC⊥BC
∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,
∴BC⊥平面PAC
∵PA?平面PAC,
∴PA⊥BC.
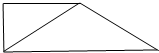
(2)该几何体的主视图如下:
∵PA=PC,取AC的中点D,连接PD,则PD⊥AC,又平面PAC⊥平面ABC,则PD⊥平面ABC,
∴几何体左视图的面积=
×AC×PD=
×1×PD=
∴PD=
,并易知△PAC是边长为1的正三角形,
∴主视图的面积是上、下底边长分别为1和2,PD的长为高的直角梯形的面积,
∴S=
×
=
(3)取PC的中点N,连接AN,由△PAC是边长为1的正三角形,可知AN⊥PC,由(1)BC⊥平面PAC,可知AN⊥BC,
∴AN⊥平面PCBM,
∴AN是四棱锥A-PCBM的高且AN=
由BC⊥平面PAC,可知BC⊥PC,
由PM∥BC可知四边形PCBM是上、下底边长分别为1和2,PC的长1为高的直角梯形,其面积S′=
.
∴V=
S′×AN=
| 5 |
∴AC2+BC2=AB2,∴AC⊥BC
∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,
∴BC⊥平面PAC
∵PA?平面PAC,
∴PA⊥BC.
(2)该几何体的主视图如下:

∵PA=PC,取AC的中点D,连接PD,则PD⊥AC,又平面PAC⊥平面ABC,则PD⊥平面ABC,
∴几何体左视图的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
∴PD=
| ||
| 2 |
∴主视图的面积是上、下底边长分别为1和2,PD的长为高的直角梯形的面积,
∴S=
| 1+2 |
| 2 |
| ||
| 2 |
3
| ||
| 4 |
(3)取PC的中点N,连接AN,由△PAC是边长为1的正三角形,可知AN⊥PC,由(1)BC⊥平面PAC,可知AN⊥BC,
∴AN⊥平面PCBM,
∴AN是四棱锥A-PCBM的高且AN=
| ||
| 2 |
由BC⊥平面PAC,可知BC⊥PC,
由PM∥BC可知四边形PCBM是上、下底边长分别为1和2,PC的长1为高的直角梯形,其面积S′=
| 3 |
| 2 |
∴V=
| 1 |
| 3 |
| ||
| 4 |
点评:本题考查了面面垂直的性质定理,线面垂直的性质,三视图的画法,以及椎体体积的计算公式,空间想象能力

练习册系列答案
相关题目

 ⊥平面
⊥平面 ,
, 为平行四边形,
为平行四边形, 分别为
分别为 的中点,
的中点, ,
, ,
,
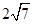 .
. ∥平面
∥平面 =90°,求证
=90°,求证 ;
;
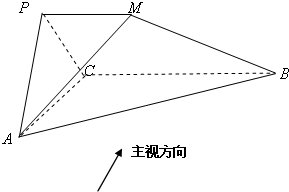
 如图所示几何体中,平面PAC⊥平面ABC,PM∥BC,PA=PC,AC=1,BC=2PM=2,AB=
如图所示几何体中,平面PAC⊥平面ABC,PM∥BC,PA=PC,AC=1,BC=2PM=2,AB= ,若该几何体左视图(侧视图)的面积为
,若该几何体左视图(侧视图)的面积为 .
. ,若该几何体左视图(侧视图)的面积为
,若该几何体左视图(侧视图)的面积为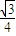 .
.