题目内容
已知二次函数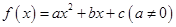 ,且不等式
,且不等式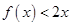 的解集为
的解集为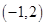 .
.
(1)方程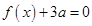 有两个相等的实根,求
有两个相等的实根,求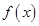 的解析式;
的解析式;
(2)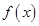 的最小值不大于
的最小值不大于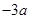 ,求实数
,求实数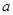 的取值范围;
的取值范围;
(3)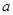 如何取值时,函数
如何取值时,函数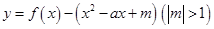 存在零点,并求出零点.
存在零点,并求出零点.
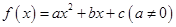 ,且不等式
,且不等式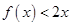 的解集为
的解集为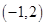 .
.(1)方程
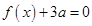 有两个相等的实根,求
有两个相等的实根,求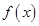 的解析式;
的解析式;(2)
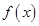 的最小值不大于
的最小值不大于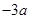 ,求实数
,求实数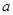 的取值范围;
的取值范围;(3)
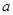 如何取值时,函数
如何取值时,函数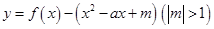 存在零点,并求出零点.
存在零点,并求出零点.(1)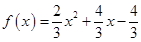 ;(2)实数
;(2)实数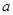 的取值范围是
的取值范围是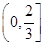 ;(3)详见解析.
;(3)详见解析.
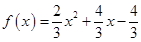 ;(2)实数
;(2)实数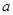 的取值范围是
的取值范围是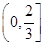 ;(3)详见解析.
;(3)详见解析.试题分析:(1)根据不等式
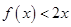 的解集为
的解集为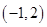 得到
得到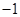 、
、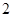 为方程
为方程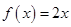 的实根,结合韦达定理确定
的实根,结合韦达定理确定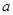 、
、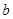 、
、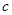 之间的等量关系以及
之间的等量关系以及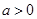 这一条件,然后利用
这一条件,然后利用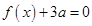 有两个相等的实根得到
有两个相等的实根得到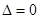 ,从而求出
,从而求出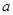 、
、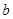 、
、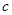 的值,最终得到函数
的值,最终得到函数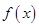 的解析式;(2)在
的解析式;(2)在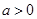 的条件下,利用二次函数的最值公式求二次函数
的条件下,利用二次函数的最值公式求二次函数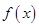 的最小值,然后利用已知条件列有关参数
的最小值,然后利用已知条件列有关参数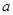 的不等式,进而求解实数
的不等式,进而求解实数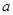 ;(3)先求出函数
;(3)先求出函数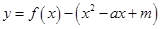 的解析式,对首项系数为零与不为零进行两种情况的分类讨论,在首项系数为零的前提下,直接将
的解析式,对首项系数为零与不为零进行两种情况的分类讨论,在首项系数为零的前提下,直接将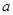 代入函数解析式,求处对应的零点;在首项系数不为零的前提下,求出
代入函数解析式,求处对应的零点;在首项系数不为零的前提下,求出 ,
,对
 的符号进行三中情况讨论,从而确定函数
的符号进行三中情况讨论,从而确定函数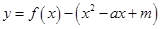 的零点个数,并求出相应的零点.
的零点个数,并求出相应的零点.试题解析:(1)由于不等式的解集为
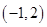 ,
,即不等式
 的解集为
的解集为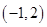 ,
,故
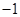 、
、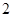 为方程
为方程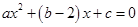 的两根,且
的两根,且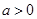 ,
,由韦达定理得
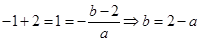 ,
,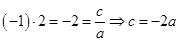 ,
,由于方程
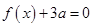 有两个相等的实根,即方程
有两个相等的实根,即方程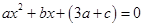 有两个相等的实根,
有两个相等的实根,则
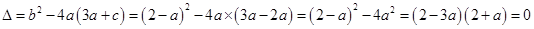 ,
,由于
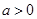 ,解得
,解得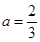 ,
,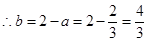 ,
,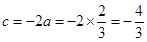 ,
,所以
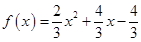 ;
;(2)由题意知,
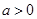 ,
, ,
,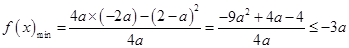 ,由于
,由于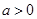 ,则有
,则有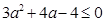 ,
,解得
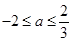 ,由于
,由于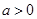 ,所以
,所以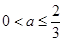 ,即实数
,即实数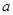 的取值范围是
的取值范围是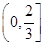 ;
;(3)
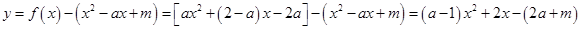 (※)
(※)①当
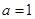 时,方程为
时,方程为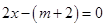 ,方程有唯一实根
,方程有唯一实根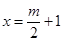 ,
,即函数
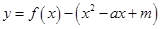 有唯一零点
有唯一零点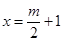 ;
;②当
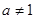 时,
时,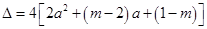 ,
,方程(※)有一解
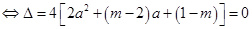 ,令
,令 ,
,得
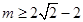 或
或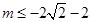 ,
,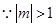 ,即
,即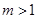 或
或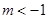 ,
,(i)当
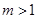 时,
时,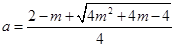 (
(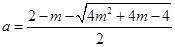 (负根舍去)),
(负根舍去)),函数
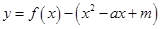 有唯一零点
有唯一零点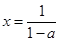 ;
;(ii)当
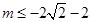 时,
时,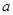 的两根都是正数,
的两根都是正数,所以当
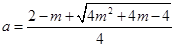 或
或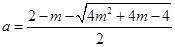 时,
时,函数
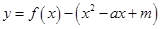 有唯一零点
有唯一零点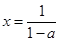 ;
;(iii)当
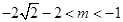 时,
时,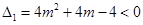 ,
,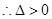 ,
,③方程(※)有二解
 ,
,(i)若
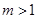 ,
,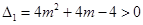 ,
,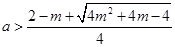 时,
时,(
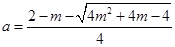 (负根舍去)),函数
(负根舍去)),函数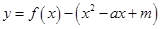 有两个零点,
有两个零点,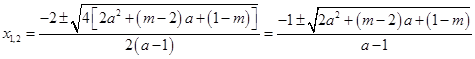 ;
;(ii)当
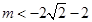 时,
时,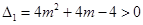 ,
,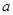 的两根都是正数,
的两根都是正数,当
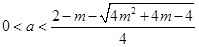 或
或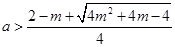 时,
时,(i)函数数
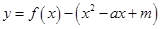 有两个零点
有两个零点 ;
;(ii)当
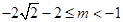 时,
时,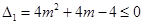 ,
,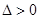 恒成立,
恒成立,所以
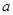 大于
大于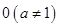 的任意实数,函数
的任意实数,函数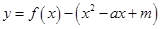 有两个零点
有两个零点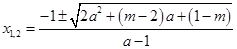 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
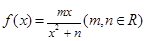 在
在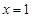 处取得极值
处取得极值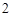 .
.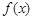 的解析式;
的解析式; 是曲线
是曲线 上除原点
上除原点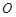 外的任意一点,过
外的任意一点,过 的中点且垂直于
的中点且垂直于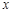 轴的直线交曲线于点
轴的直线交曲线于点 ,试问:是否存在这样的点
,试问:是否存在这样的点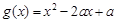 ,若对于任意
,若对于任意 ,总存在
,总存在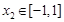 ,使得
,使得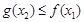 ,求实数
,求实数 的取值范围.
的取值范围. ,其中a是实数.设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的两点,且x1<x2.
,其中a是实数.设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的两点,且x1<x2.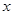 ,使
,使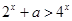 成立,则实数
成立,则实数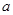 的取值范围是 .
的取值范围是 .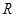 上的函数
上的函数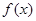 是周期为
是周期为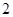 的偶函数,当
的偶函数,当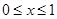 时,
时,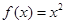 ,如果直线
,如果直线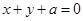 与曲线
与曲线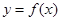 恰有两个交点,则实数
恰有两个交点,则实数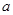 的值是( )
的值是( )
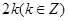
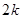 或
或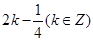
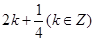
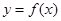 对任意的
对任意的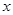 都满足
都满足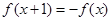 ,当
,当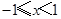 时,
时,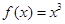 ,若函数
,若函数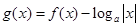 至少6个零点,则
至少6个零点,则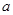 取值范围是( )
取值范围是( )
 上是增函数,则
上是增函数,则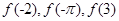 的大小关系是( )
的大小关系是( )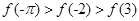
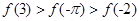
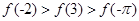
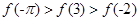
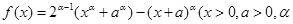 为有理数且
为有理数且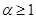 ),求函数
),求函数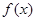 的最小值;
的最小值;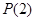 :设
:设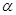 为有理数且
为有理数且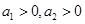 时,则
时,则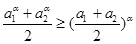 ;
;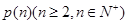 ,并证明你的结论;
,并证明你的结论;