题目内容
(本小题满分12分)已知向量 =3i-4j,
=3i-4j, =6i-3j,
=6i-3j, =(5-m)i-(3+m)j其中i,j分别是直角坐标系内x轴与y轴正方向上的单位向量
=(5-m)i-(3+m)j其中i,j分别是直角坐标系内x轴与y轴正方向上的单位向量
(1)A,B,C能够成三角形,求实数m应满足的条件。
(2)对任意m∈[1,2]使不等式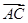 2≤-x2+x+3恒成立,求x的取值范围
2≤-x2+x+3恒成立,求x的取值范围
(1) ;(2)
;(2) 的取值范围是
的取值范围是 .
.
解析试题分析:(1)
 不共线,
不共线, ……………………………………………-…………………4分
……………………………………………-…………………4分
(2)因为 ,
,
所以,当 或
或 时,
时, 最大,最大值是
最大,最大值是 ,………………………………………9分
,………………………………………9分
所以, ,即
,即 的取值范围是
的取值范围是 .……………………………………12分
.……………………………………12分
考点:本题主要考查平面向量的坐标运算,共线向量的条件,一元二次不等式解法。
点评:中档题,本题解的思路比较明确,(1)注意到 不共线,(2)注意
不共线,(2)注意 ,转化得到一元二次不等式。
,转化得到一元二次不等式。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设P是△ABC所在平面内的一点, ,则( )
,则( )
A. | B. | C. | D. |

 ;
; ,求k的值.
,求k的值.

 时,求
时,求 的值;
的值;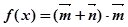 ,求
,求 的单调增区间;
的单调增区间; 中,
中, 分别为角
分别为角 的对边,
的对边, ,对于(2)中的函数
,对于(2)中的函数 的取值范围。
的取值范围。 的面积
的面积 满足
满足 ,
, 的夹角为
的夹角为 .
. 的最大值.
的最大值. ,设函数
,设函数 ,(Ⅰ)求函数
,(Ⅰ)求函数 的表达式;(Ⅱ)在
的表达式;(Ⅱ)在 中,
中, 分别是角
分别是角 的对边,
的对边, 为锐角,若
为锐角,若
 ,
, ,
, ,求边
,求边 的长.
的长. ;(1)求:AB2+AC2的值;(2)当△ABC的面积最大时,求A的大小.
;(1)求:AB2+AC2的值;(2)当△ABC的面积最大时,求A的大小. 的模均为1,它们相互之间的夹角均为
的模均为1,它们相互之间的夹角均为 。
。 ;
;
 ,求
,求 的取值范围。
的取值范围。