题目内容
(本小题满分12分) 已知向量 ,设函数
,设函数 ,(Ⅰ)求函数
,(Ⅰ)求函数 的表达式;(Ⅱ)在
的表达式;(Ⅱ)在 中,
中, 分别是角
分别是角 的对边,
的对边, 为锐角,若
为锐角,若
 ,
, ,
, 的面积为
的面积为 ,求边
,求边 的长.
的长.
(Ⅰ)f(x) ;(Ⅱ)边
;(Ⅱ)边 的长为5。
的长为5。
解析试题分析:(Ⅰ)由题意得:

(Ⅱ)由
 得:
得: ,化简得:
,化简得: , 又因为
, 又因为 ,解得:
,解得:
由题意知: ,解得
,解得 ,
,
又 ,所以
,所以
 故所求边
故所求边 的长为5。
的长为5。
考点:本题主要考查正弦定理;平面向量数量积的运算;两角和与差的正弦函数.
点评:本题综合考查了平面向量的数量积运算,二倍角的正弦函数公式,两角和与差的正弦函数公式,三角形的面积公式,以及特殊角的三角函数值,熟练掌握公式及法则是解本题的关键.

练习册系列答案
相关题目

 若
若 ,求
,求 的值;
的值; 求
求 的最大值
的最大值
 中,
中, 分别是角
分别是角 所对的边
所对的边
 中,
中,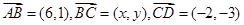 .
.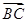 ∥
∥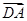 ,试求
,试求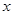 与
与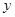 满足的关系
满足的关系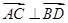 ,求
,求 =3i-4j,
=3i-4j, =6i-3j,
=6i-3j, =(5-m)i-(3+m)j其中i,j分别是直角坐标系内x轴与y轴正方向上的单位向量
=(5-m)i-(3+m)j其中i,j分别是直角坐标系内x轴与y轴正方向上的单位向量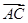 2≤-x2+x+3恒成立,求x的取值范围
2≤-x2+x+3恒成立,求x的取值范围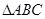 的角A、B、C所对的边分别是
的角A、B、C所对的边分别是 ,设向量
,设向量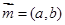 ,
, 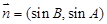 ,
, 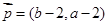
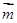 ∥
∥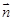 ,求证:
,求证: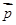 ,边长
,边长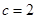 ,
,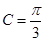 ,求
,求 ,
, 的最大值和最小值;
的最大值和最小值; ,求k的取值范围。
,求k的取值范围。 ,A、B、C在一条直线上,且
,A、B、C在一条直线上,且 ,则( ).
,则( ).
 B、
B、
 D、
D、
 ,直线
,直线 与抛物线
与抛物线 交于
交于 两点,
两点, ,
, ,
, 与
与 .
.
 的面积的最小值.
的面积的最小值.