题目内容
方程sinx+cosx=k在[0,π]上有两个解,则k的取值范围为( )
分析:设y1=sinx+cosx,y2=k,方程sinx+cosx=k在[0,π]上有两个解转化为函数y1=
sin(x+
),x∈[0,π]的图象与直线y2=k有两个交点,数形结合即可求得k的取值范围.
| 2 |
| π |
| 4 |
解答:解:设y1=sinx+cosx=
(
sinx+
cosx)
=
(sinxcos
+cosxsin
)
=
sin(x+
),
∵x∈[0,π],
∴
≤x+
≤
,
∴
≤sin(x+
)≤1,1≤
sin(x+
)≤
;
再令y2=k,
则方程sinx+cosx=k在[0,π]上有两个解等价于函数y1=
sin(x+
),x∈[0,π]的图象与直线y2=k有两个交点,
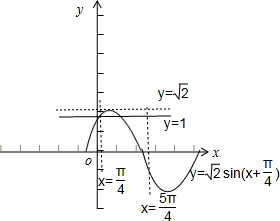
∴1≤k<
.
故选D.
| 2 |
| ||
| 2 |
| ||
| 2 |
=
| 2 |
| π |
| 4 |
| π |
| 4 |
=
| 2 |
| π |
| 4 |
∵x∈[0,π],
∴
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
∴
| ||
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
| 2 |
再令y2=k,
则方程sinx+cosx=k在[0,π]上有两个解等价于函数y1=
| 2 |
| π |
| 4 |
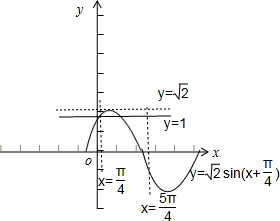
∴1≤k<
| 2 |
故选D.
点评:本题考查正弦函数的图象与性质,考查辅助角公式的应用,考查数形结合思想,属于中档题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案
相关题目
方程
=k(k>0)有且仅有两个不同的实数解θ,φ(θ>φ),则以下有关两根关系的结论正确的是( )
| |sinx| |
| x |
| A、sinφ=φcosθ |
| B、sinφ=-φcosθ |
| C、cosφ=θsinθ |
| D、sinθ=-θsinφ |