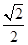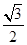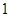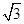题目内容
已知F1、F2分别是双曲线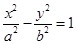 的左、右焦点,P为双曲线右支上的任意一点且
的左、右焦点,P为双曲线右支上的任意一点且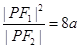 ,则双曲线离心率的取值范围是( )
,则双曲线离心率的取值范围是( )
| A.(1,2] | B.[2 +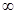 ) ) | C.(1,3] | D.[3,+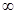 ) ) |
C
解析试题分析:由定义知:|PF1|-|PF2|=2a,所以|PF1|=2a+|PF2|, +4a+|PF2| ≥8a,当且仅当
+4a+|PF2| ≥8a,当且仅当 =|PF2|,即|PF2|=2a时取得等号,设P(x0,y0) (x0
=|PF2|,即|PF2|=2a时取得等号,设P(x0,y0) (x0 a),由焦半径公式得:|PF2|=-ex0-a=2a,
a),由焦半径公式得:|PF2|=-ex0-a=2a, ,又双曲线的离心率e>1,∴e∈(1,3],故选C.
,又双曲线的离心率e>1,∴e∈(1,3],故选C.
考点:本题主要考查双曲线的定义及几何性质,均值定理的应用

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
已知F为抛物线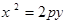
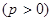 的焦点,M为其上一点,且
的焦点,M为其上一点,且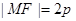 ,则直线MF的斜率为( ).
,则直线MF的斜率为( ).
A.-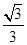 | B.±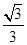 | C.-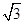 | D.±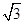 |
给出如下四个命题:
①若“”为假命题,则均为假命题;
②命题“若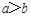 ,则
,则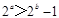 ”的否命题为“若
”的否命题为“若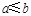 ,则
,则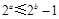 ”;
”;
③命题“任意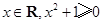 ”的否定是“存在
”的否定是“存在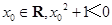 ”;
”;
④在中,“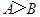 ”是“
”是“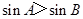 ”的充要条件.
”的充要条件.
其中不正确命题的个数是 ( )
| A.4 | B.3 | C.2 | D.1 |
已知椭圆E: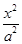 +
+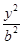 =1(a>b>0)的右焦点为F(3,0),过点F的直线交E于A,B两点.若AB的中点坐标为(1,-1),则E的方程为( )
=1(a>b>0)的右焦点为F(3,0),过点F的直线交E于A,B两点.若AB的中点坐标为(1,-1),则E的方程为( )
A.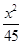 + +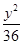 =1 =1 | B.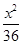 + +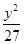 =1 =1 | C.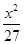 + +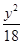 =1 =1 | D. + +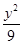 =1 =1 |
已知抛物线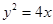 的焦点
的焦点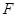 与双曲线
与双曲线 的一个焦点重合,它们在第一象限内的交点为
的一个焦点重合,它们在第一象限内的交点为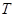 ,且
,且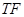 与
与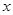 轴垂直,则此双曲线的离心率为( )
轴垂直,则此双曲线的离心率为( )
A.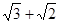 | B.2 | C.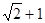  | D.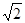 |
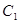 与双曲线
与双曲线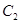 有共同的焦点
有共同的焦点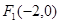 ,
,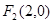 ,椭圆的一个短轴端点为
,椭圆的一个短轴端点为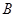 ,直线
,直线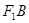 与双曲线的一条渐近线平行,椭圆
与双曲线的一条渐近线平行,椭圆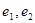 ,则
,则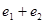 取值范围为( )
取值范围为( )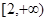
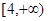
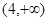
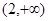
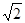
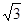
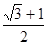
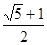
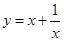 是一个对称轴不在坐标轴上的双曲线,它的渐近线分别是
是一个对称轴不在坐标轴上的双曲线,它的渐近线分别是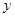 轴和直线
轴和直线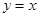 ,其离心率e=( )
,其离心率e=( )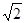
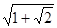
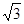
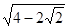
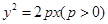 的焦点为
的焦点为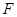 ,已知点
,已知点 为抛物线上的两个动点,且满足
为抛物线上的两个动点,且满足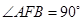 .过弦
.过弦 的中点
的中点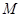 作抛物线准线的垂线
作抛物线准线的垂线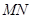 ,垂足为
,垂足为 ,则
,则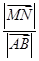 的最大值为( )
的最大值为( )