题目内容
已知等差数列![]() 的首项
的首项![]() =1,公差d>0,且第2项、第5项、第14项分别为等比数列
=1,公差d>0,且第2项、第5项、第14项分别为等比数列![]() 的第2项、第3项、第4项。
的第2项、第3项、第4项。
(1)求数列![]() 与
与![]() 的通项公式;
的通项公式;
(2)设数列{![]() }对n
}对n![]()
![]() 均有
均有![]() +
+![]() +…+
+…+![]() =
=![]() 成立,求
成立,求![]() +
+![]()
![]() +…+
+…+![]() 。
。
解答:(1)由已知得![]() =1+d,
=1+d, ![]() =1+4d,
=1+4d, ![]() =1+13d, ………1分
=1+13d, ………1分
![]()
![]() =(1+d)(1+13d),
=(1+d)(1+13d), ![]() d=2,
d=2, ![]() =2n-1 …………3分
=2n-1 …………3分
又![]() =
=![]() =3,
=3,![]() =
= ![]() =9
=9 ![]() 数列{
数列{![]() }的公比为
}的公比为![]() 3,
3,
![]() =3
=3![]()
![]() =
=![]() . ……………6分
. ……………6分
(2)由![]() +
+![]() +…+
+…+![]() =
=![]() (1)
(1)
当n=1时,![]() =
=![]() =3,
=3, ![]()
![]() =3 ……………8分
=3 ……………8分
当n>1时,![]() +
+![]() +…+
+…+![]() =
= ![]() (2) ……………9分
(2) ……………9分
(1)-(2)得 ![]() =
=![]() -
-![]() =2 ……………10分
=2 ……………10分
![]()
![]() =2
=2![]() =2
=2![]()
![]() 对
对![]() 不适用
不适用
![]()
![]() =
=![]() ……………12分
……………12分
![]()
![]() …
…![]() =3+2
=3+2![]() 3+2
3+2![]()
![]() +…+2
+…+2![]()
![]()
=1+2![]() 1+2
1+2![]() 3+2
3+2![]()
![]() +…+2
+…+2![]()
![]() =1+2
=1+2![]()
![]() =
=![]() .
.

练习册系列答案
相关题目
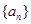 的首项
的首项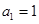 ,公差
,公差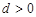 .且
.且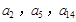 分别是等比数列
分别是等比数列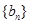 的
的 .
.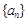 与
与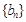 的通项公式;
的通项公式;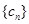 对任意自然数
对任意自然数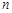 均有
均有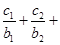
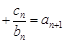 成立,求
成立,求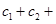
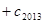 的值.
的值.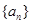 的首项
的首项 ,公差
,公差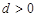 .且
.且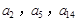 分别是等比数列
分别是等比数列 的
的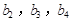 .
. 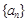 与
与 对任意自然数
对任意自然数 均有
均有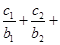
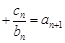 成立,求
成立,求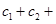
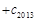 的值.
的值. 的首项为
的首项为 ,公差为
,公差为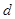 ,其前
,其前 项和为
项和为 ,若直线
,若直线 与圆
与圆 的两个交点关于直线
的两个交点关于直线 对称,则
对称,则 的首项为
的首项为 ,公差为b,且不等式
,公差为b,且不等式 的解集为
的解集为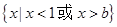 .
. 公式 ;
公式 ; 

 的前n项和Tn .
的前n项和Tn .