题目内容
已知等差数列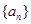 的首项
的首项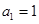 ,公差
,公差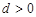 .且
.且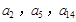 分别是等比数列
分别是等比数列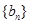 的
的 .
.
(1)求数列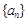 与
与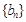 的通项公式;
的通项公式;
(2)设数列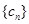 对任意自然数
对任意自然数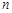 均有
均有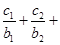
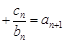 成立,求
成立,求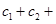
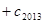 的值.
的值.
【答案】
(1)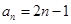 ,
,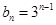 ;(2)
;(2)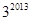 .
.
【解析】
试题分析:本题考查等差数列与等比数列的通项公式、前n项和公式等基础知识,考查思维能力、分析问题与解决问题的能力.第一问,先用等差数列的通项公式将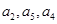 展开,因为
展开,因为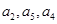 成等比,利用等比中项列等式求
成等比,利用等比中项列等式求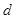 ,直接写出
,直接写出 的通项公式,通过求出来的
的通项公式,通过求出来的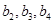 得出
得出 和
和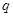 ,写出数列
,写出数列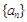 与
与 的通项公式;第二问,用
的通项公式;第二问,用 代替已知等式中的
代替已知等式中的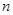 ,得到新的等式,2个等式相减,把第一问的2通项公式代入得到
,得到新的等式,2个等式相减,把第一问的2通项公式代入得到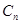 的通项公式,注意
的通项公式,注意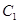 的检验,最后利用等比数列的求和公式求和.
的检验,最后利用等比数列的求和公式求和.
试题解析:(1) ∵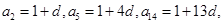 且
且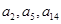 成等比数列
成等比数列
∴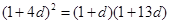 ,即
,即 ,
,
∴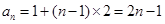 ,
,
又∵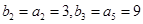 ,
,
∴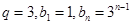 .
.
(2)∵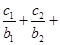
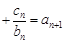 ①
①
∴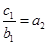 即
即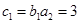 ,又
,又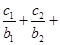
 ②
②
①-②:
∴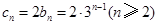 10分
10分
∴ 11分
11分
则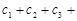
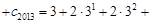
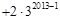
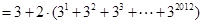
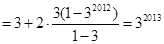 12分
12分
考点:1.等差数列的通项公式;2.等比中项;3.等比数列的前n项和公式.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
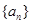 的首项
的首项 ,公差
,公差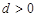 .且
.且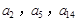 分别是等比数列
分别是等比数列 的
的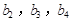 .
. 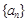 与
与 对任意自然数
对任意自然数 均有
均有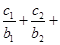
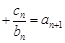 成立,求
成立,求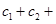
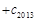 的值.
的值. 的首项为
的首项为 ,公差为
,公差为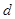 ,其前
,其前 项和为
项和为 ,若直线
,若直线 与圆
与圆 的两个交点关于直线
的两个交点关于直线 对称,则
对称,则 的首项为
的首项为 ,公差为b,且不等式
,公差为b,且不等式 的解集为
的解集为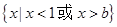 .
. 公式 ;
公式 ; 

 的前n项和Tn .
的前n项和Tn .