题目内容
已知等差数列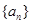 的首项
的首项 ,公差
,公差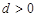 .且
.且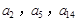 分别是等比数列
分别是等比数列 的
的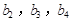 .
.
(Ⅰ)求数列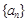 与
与 的通项公式;
的通项公式;
(Ⅱ)设数列 对任意自然数
对任意自然数 均有
均有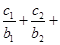
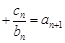 成立,求
成立,求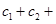
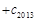 的值.
的值.
【答案】
(Ⅰ) ,
,  ;(Ⅱ)
;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)根据等比中项的定义列出等式,求出等差数列 的公差,从而求出数列
的公差,从而求出数列 的公比
的公比 ,便可得到通向公式;(Ⅱ)按已知等式的规律写出
,便可得到通向公式;(Ⅱ)按已知等式的规律写出 ,再两式相减,得出数列
,再两式相减,得出数列 即是等差数列,变形求得数列
即是等差数列,变形求得数列 的通向公式,用公式求和.
的通向公式,用公式求和.
试题解析:(Ⅰ)∵ ,
, ,
, ,且
,且 成等比数列
成等比数列
∴  2分
2分
∴ 4分
4分
又∵ .
.
∴ 6分
6分
(Ⅱ)∵
 ①
①
∴ 即
即
又
 ②
②
①-②: 8分
8分
∴
∴  10分
10分
则



 12分
12分
考点:等差数列、等比数列的性质,求和公式.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
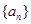 的首项
的首项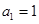 ,公差
,公差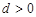 .且
.且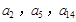 分别是等比数列
分别是等比数列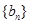 的
的 .
.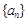 与
与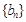 的通项公式;
的通项公式;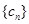 对任意自然数
对任意自然数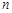 均有
均有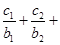
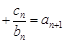 成立,求
成立,求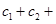
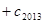 的值.
的值. 的首项为
的首项为 ,公差为
,公差为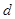 ,其前
,其前 项和为
项和为 ,若直线
,若直线 与圆
与圆 的两个交点关于直线
的两个交点关于直线 对称,则
对称,则 的首项为
的首项为 ,公差为b,且不等式
,公差为b,且不等式 的解集为
的解集为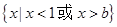 .
. 公式 ;
公式 ; 

 的前n项和Tn .
的前n项和Tn .