题目内容
将函数f（x）=sin2x的图象按向量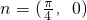
平移得到g（x）的图象，则函数f（x）与g（x）的图象
- A.关于直线
对称 - B.关于直线
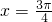对称 - C.关于直线
对称 - D.关于y轴对称
A
分析：先确定向量a的方向，然后按照左加右减的原则进行平移可得g（x），然后根据对称性可求两函数的对称直线
解答：∵函数f（x）=sin2x的图象按向量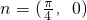平移即是向右平移
个单位
∴g（x）=f（x-）=sin2（x-）=-cos2x
设函数f（x）=sin2x与g（x）=-cos2x的图象关于x=a对称，
则在f（x）=sin2x任取一定M（x，y）其关于x=a对称的点（x′，y′）在g（x）=-cos2x上
∵
∴y′=sin（4a-2x′）=-cos2x′
结合选项代入验证知，当x=
时，sin（
）=-cos2x′复合条件
故选A
点评：本题主要考查三角函数y=Asin（ωx+∅）的图象变换以及平面向量坐标表示的应用，判断把函数y=sin2x的图象按照向量平移后可得函数y=g（x）的图象，是解题的突破
分析：先确定向量a的方向，然后按照左加右减的原则进行平移可得g（x），然后根据对称性可求两函数的对称直线
解答：∵函数f（x）=sin2x的图象按向量
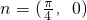平移即是向右平移个单位∴g（x）=f（x-
）=sin2（x-）=-cos2x设函数f（x）=sin2x与g（x）=-cos2x的图象关于x=a对称，
则在f（x）=sin2x任取一定M（x，y）其关于x=a对称的点（x′，y′）在g（x）=-cos2x上
∵
∴y′=sin（4a-2x′）=-cos2x′
结合选项代入验证知，当x=
时，sin（）=-cos2x′复合条件故选A
点评：本题主要考查三角函数y=Asin（ωx+∅）的图象变换以及平面向量坐标表示的应用，判断把函数y=sin2x的图象按照向量平移后可得函数y=g（x）的图象，是解题的突破
练习册系列答案
相关题目
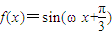（ω＞0）的图象的相邻两条对称轴间的距离是
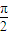．若将函数f（x）图象向右平移
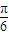个单位，得到函数g（x）的解析式为（ ）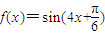
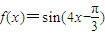
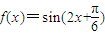
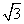sinωx·sin（ωx+
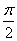）+2cos2ωx，x∈R（ω>0），在y轴右侧的第一个最高点的横坐标为
。
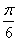个单位，则所得到的图象对应的函数的一个单调递增区间是 （ ）
） C．（
） D．（