题目内容
已知函数![]() .
.
(1)当![]() 时,指出
时,指出![]() 的单调递减区间和奇偶性(不需说明理由);
的单调递减区间和奇偶性(不需说明理由);
(2)当![]() 时,求函数
时,求函数![]() 的零点;
的零点;
(3)若对任何![]() 不等式
不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
解: 1)当![]() 时,函数的单调递减区间为
时,函数的单调递减区间为![]() (2分)
(2分)
函数![]() 既不是奇函数也不是偶函数(4分)
既不是奇函数也不是偶函数(4分)
(2)当![]() ,(1分)
,(1分)
由![]() 得
得![]() (2分)
(2分)
即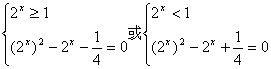 (4分)
(4分)
解得![]() (5分)
(5分)
所以![]() 或
或![]() (6分)
(6分)
(3)当![]() 时,
时,![]() 取任意实数,不等式
取任意实数,不等式![]() 恒成立,
恒成立,
故只需考虑![]() ,此时原不等式变为
,此时原不等式变为![]() (1分)
(1分)
即![]()
故![]() (2分)
(2分)
又函数![]() 在
在![]() 上单调递增,
上单调递增,![]() (3分)
(3分)
函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,(4分)
上单调递增,(4分)
![]() ;(5分)
;(5分)
所以![]() ,即实数
,即实数![]() 的取值范围是
的取值范围是![]() (6分)
(6分)

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 ,
, 。
。 的单调区间;
的单调区间; 时,
时, 对任意正实数
对任意正实数 都成立;
都成立; ,使得
,使得 对任意的正实数
对任意的正实数 都成立,请直接写出满足这样条件的一个
都成立,请直接写出满足这样条件的一个 。
。 在区间
在区间 上的取值范围;
(2) 当
上的取值范围;
(2) 当 时,
时,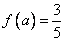 ,求m的值。
,求m的值。