题目内容
已知函数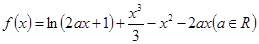
(I)若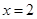 为
为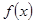 的极值点,求实数
的极值点,求实数 的值;
的值;
(II)若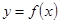 在
在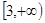 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围;
(Ⅲ)当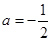 时,方程
时,方程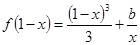 有实根,求实数
有实根,求实数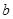 的最大值。
的最大值。
(I)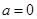 (II)
(II)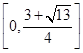 (Ⅲ) 实数
(Ⅲ) 实数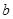 的最大值为0
的最大值为0
解析试题分析:(I)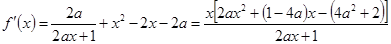
因为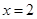 为
为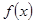 的极值点,所以
的极值点,所以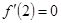 ,即
,即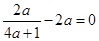 ,
,
解得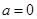 。经检验,合题意
。经检验,合题意
(II)因为函数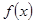 在
在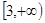 上为增函数,所以
上为增函数,所以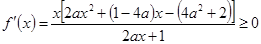 在
在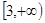 上恒成立。
上恒成立。
?当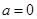 时,
时,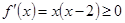 在
在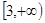 上恒成立,所以
上恒成立,所以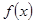 在
在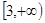 上为增函数,故
上为增函数,故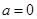 符合题意。 6分
符合题意。 6分
?当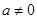 时,由函数
时,由函数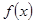 的定义域可知,必须有
的定义域可知,必须有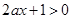 对
对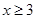 恒成立,
恒成立,
故只能 ,所以
,所以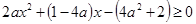 在
在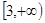 上恒成立。
上恒成立。
令函数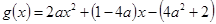 ,其对称轴为
,其对称轴为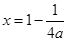 ,
,
因为 ,所以
,所以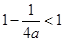 ,
,
要使 在
在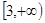 上恒成立,
上恒成立,
只要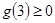 即可,即
即可,即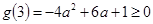 ,
,
所以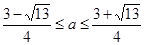 。
。
因为 ,所以
,所以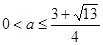 。
。
综上所述,a的取值范围为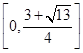 。
。
(Ⅲ)当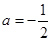 时,方程
时,方程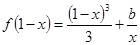 可化为
可化为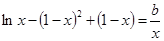 。
。
问题转化为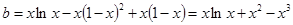 在
在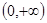 上有解,即求函数
上有解,即求函数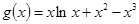 的值域。
的值域。
因为函数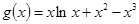 ,令函数
,令函数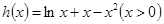 ,
,
则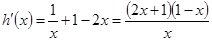 ,
,
所以当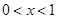 时,
时,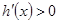 ,从而函数
,从而函数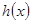 在
在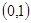 上为增函数,
上为增函数,
当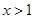 时,
时,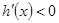 ,从而函数
,从而函数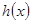 在
在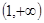 上为减函数,
上为减函数,
因此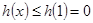 。
。
而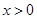 ,所以
,所以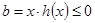 ,因此当
,因此当 时,b取得最大值0.
时,b取得最大值0.
考点:本小题主要考查导数在研究函数性质中的应用,考查学生分类讨论思想的应用.
点评:导数是研究函数性质的有力工具,求极值时要注意验根,因为极值点处的导数值为0,但是导数值为0的点不一定是极值点,涉及到含参数问题,一般离不开分类讨论,分类标准要尽量做到不重不漏.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在(1,2)上是增函数,
在(1,2)上是增函数,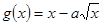 在(0,1)上是减函数。
在(0,1)上是减函数。 求
求 的值;
的值; 当
当 时,若
时,若 在
在 内恒成立,求实数
内恒成立,求实数 的取值范围;
的取值范围; 求证:方程
求证:方程 在
在 内有唯一解.
内有唯一解. ,求
,求
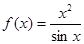 ,求
,求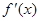
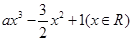 ,其中a>0,
,其中a>0, 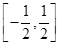 上,f(x)>0恒成立,求a的取值范围。
上,f(x)>0恒成立,求a的取值范围。 。
。 的单调递减区间;
的单调递减区间; 的切线方程;
的切线方程; 上的最大值与最小值。
上的最大值与最小值。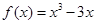
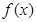 的单调区间;(2)求
的单调区间;(2)求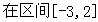 上的最小值.
上的最小值.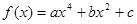 的图象经过点
的图象经过点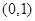 ,且在
,且在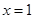 处的切线方程是
处的切线方程是 .
.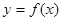 的解析式;
的解析式; ,
,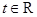 .
.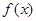 的极值点;
的极值点; 对
对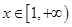 恒成立,求实数
恒成立,求实数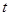 的取值范围.
的取值范围.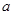 为实数,
为实数,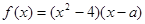
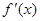 ;
;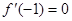 ,求
,求 在[-2,2] 上的最大值和最小值;
在[-2,2] 上的最大值和最小值;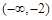 和
和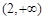 上都是递增的,求
上都是递增的,求