题目内容
已知函数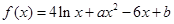 (
(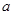 ,
,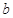 为常数),且
为常数),且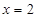 为
为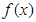 的一个极值点.
的一个极值点.
(Ⅰ) 求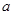 的值;
的值;
(Ⅱ) 求函数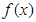 的单调区间;
的单调区间;
(Ⅲ) 若函数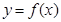 有3个不同的零点,求实数
有3个不同的零点,求实数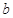 的取值范围.
的取值范围.
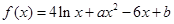 (
(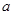 ,
,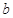 为常数),且
为常数),且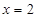 为
为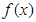 的一个极值点.
的一个极值点.(Ⅰ) 求
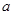 的值;
的值;(Ⅱ) 求函数
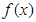 的单调区间;
的单调区间;(Ⅲ) 若函数
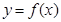 有3个不同的零点,求实数
有3个不同的零点,求实数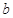 的取值范围.
的取值范围.解: (Ⅰ) 函数f (x)的定义域为(0,+∞)……1分
∵ f ′ (x) = ……….2分
……….2分
∴ ,则a = 1.……….4分
,则a = 1.……….4分
(Ⅱ)由(Ⅰ) 知
∴ f ′ (x) = ………6分
………6分
由f ′ (x) > 0可得x>2或x<1,由f ′ (x) < 0可得1< x <2.
∴ 函数f ( x ) 的单调递增区间为 (0 ,1) 和 (2,+ ∞ ),
单调递减区间为 (1 , 2 ). …9分
(Ⅲ) 由(Ⅱ)可知函数f (x)在(0,1)单调递增,在(1,2)单调递减,在(2,+∞)单调递增.
且当x =1或x =2时,f ′ (x) = 0.
∴ f (x) 的极大值为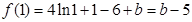 …10分
…10分
f (x)的极小值为
由题意可知
则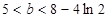 ………11分
………11分
∵ f ′ (x) =
 ……….2分
……….2分∴
 ,则a = 1.……….4分
,则a = 1.……….4分 (Ⅱ)由(Ⅰ) 知

∴ f ′ (x) =
 ………6分
………6分 由f ′ (x) > 0可得x>2或x<1,由f ′ (x) < 0可得1< x <2.
∴ 函数f ( x ) 的单调递增区间为 (0 ,1) 和 (2,+ ∞ ),
单调递减区间为 (1 , 2 ). …9分
(Ⅲ) 由(Ⅱ)可知函数f (x)在(0,1)单调递增,在(1,2)单调递减,在(2,+∞)单调递增.
且当x =1或x =2时,f ′ (x) = 0.
∴ f (x) 的极大值为
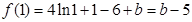 …10分
…10分 f (x)的极小值为

由题意可知

则
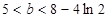 ………11分
………11分本试题主要考查了导数在研究函数中的运用,利用导数来判定函数的单调性,以及函数的零点的综合运用。
(1)函数f (x)的定义域为(0,+∞) ∵ f ′ (x) =
∴ ,则a = 1
,则a = 1
(2)由(Ⅰ) 知
∴ f ′ (x) = 解二次不等式得到单调区间。
解二次不等式得到单调区间。
(3)由(Ⅱ)可知函数f (x)在(0,1)单调递增,在(1,2)单调递减,在(2,+∞)单调递增.
且当x =1或x =2时,f ′ (x) = 0。
(1)函数f (x)的定义域为(0,+∞) ∵ f ′ (x) =

∴
 ,则a = 1
,则a = 1(2)由(Ⅰ) 知

∴ f ′ (x) =
 解二次不等式得到单调区间。
解二次不等式得到单调区间。(3)由(Ⅱ)可知函数f (x)在(0,1)单调递增,在(1,2)单调递减,在(2,+∞)单调递增.
且当x =1或x =2时,f ′ (x) = 0。

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
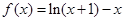
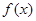 的单调递减区间;
的单调递减区间;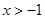 ,证明:
,证明: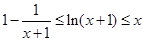 .
.  ,若a <b,且f(a)=f(b),则a+2b的取值范围是________ .
,若a <b,且f(a)=f(b),则a+2b的取值范围是________ .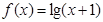 ,
,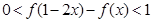 ,求
,求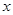 的取值范围;
的取值范围;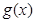 是以2为周期的偶函数,且当
是以2为周期的偶函数,且当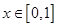 时,
时,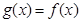 ,当
,当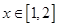 时,求函数
时,求函数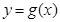 的取值范围.
的取值范围.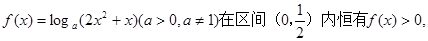 则f(x)的单调递增区间是
则f(x)的单调递增区间是 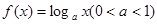 在区间
在区间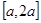 上的最大值是最小值的3倍,则
上的最大值是最小值的3倍,则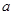


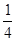

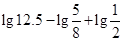 的值.
的值. 的值是_________。
的值是_________。 ,则
,则 的大小关系是 。
的大小关系是 。