题目内容
（本题满分12分）已知函数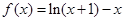
（1）求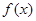
的单调递减区间；
（2）若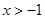
，证明：
.
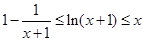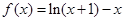
（1）求
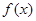的单调递减区间；（2）若
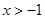，证明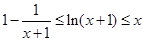：. （1）减区间为
；（2）见解析。
；（2）见解析。第一问利用导数求函数的单调递减区间，第二问是函数类不等式的证明，这类问题常常以导数为工具，利用函数的单调性来解决。
解：（1）减区间为
（2）由（1）知，当
时
，当
时，
时
即
令
，则
，当
时
；当时
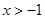综上可知，当时，有。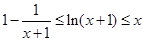
解：（1）减区间为
（2）由（1）知，当
时，当时，时即令，则，当时；当时综上可知，当
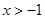时，有。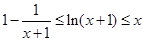
练习册系列答案
相关题目
，
之间的大小关系是（ ）
﹤
﹤
, 
,
,求
取值范围; 
的最值，并给出最值时对应的x的值。
的解集是
,则
的值为___________。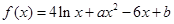
（
，
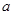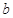为常数），且
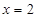为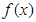
的一个极值点．
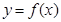有3个不同的零点，求实数
，
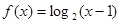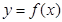的定义域；
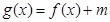，若函数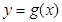
在（2，3）内有且仅有一个零点，求实数
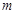的取值范围；
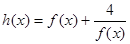，求函数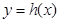
在[3，9]内的值域；
，N＝logab，P＝logb
，则
的值是（ ）
，则
的取值范围是 。