题目内容
6.已知平行四边形ABCD从平面AC外一点O引向量.$\overrightarrow{OE}$=k$\overrightarrow{OA}$,$\overrightarrow{OF}$=k$\overrightarrow{OB}$,$\overrightarrow{OG}$=k$\overrightarrow{OC}$,$\overrightarrow{OH}$=k$\overrightarrow{OD}$.(1)求证:四点E,F,G,H共面;
(2)平面AC∥平面EG.
分析 (1)可画出图形,根据$\overrightarrow{OE}=k\overrightarrow{OA},\overrightarrow{OF}=k\overrightarrow{OB}$便可得到$\frac{OE}{OA}=\frac{OF}{OB}$,从而得出EF∥AB,同理HG∥DC,且有EF=HG,这便可判断四边形EFGH为平行四边形,从而得出四点E,F,G,H共面;
(2)由上面知EF∥AB,FG∥BC,从而得出EF∥平面AC,FG∥平面AC,这样根据面面平行的判定定理即可得出平面AC∥平面EG.
解答 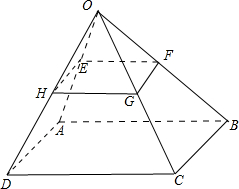 解:(1)证明:如图,
解:(1)证明:如图,
∵$\overrightarrow{OE}=k\overrightarrow{OA},\overrightarrow{OF}=k\overrightarrow{OB}$;
∴$\frac{OE}{OA}=\frac{OF}{OB}=|k|$;
EF∥AB,且EF=|k|AB;
同理HG∥DC,且HG=|k|DC,AB=DC;
∴EF∥HG,且EF=HG;
∴四边形EFGH为平行四边形;
∴四点E,F,G,H共面;
(2)由上面EF∥AB,AB?平面AC,EF?平面AC;
∴EF∥平面AC,同理FG∥BC,FG∥平面AC;
EF∩FG=F;
∴平面AC∥平面EG.
点评 考查共线向量基本定理,向量数乘的几何意义,平行线分线段成比例,以及平行四边形的概念及判断方法,线面平行和面面平行的判定定理.

练习册系列答案
相关题目
17.函数f(x)=$\frac{{\sqrt{4-{x^2}}}}{{lg({x+1})}}$的定义域为( )
| A. | [-2,0)∪(0,2] | B. | (-1,0)∪(0,2] | C. | [-2,2] | D. | (-1,2] |
1.若复数z=i(1+i),(i是虚数单位),则z的共轭复数是( )
| A. | -1+i | B. | -1-i | C. | 1+i | D. | 1-i |
15.下列各组函数是同一函数的是( )
| A. | y=1,y=$\frac{x}{x}$ | B. | y=$\sqrt{x-1}$×$\sqrt{x+1}$,y=$\sqrt{{x}^{2}-1}$ | ||
| C. | y=|x|,y=($\sqrt{x}$)2 | D. | y=x,y=$\root{3}{{x}^{3}}$ |