题目内容
16.在三棱锥A-BCD中,AB=2$\sqrt{6}$,△ACD和△BCD均是边长为4的等边三角形,则三棱锥外接球的表面积为$\frac{80π}{3}$.分析 取AB,CD中点分别为E,F,连接EF,AF,BF,求出EF,判断三棱锥的外接球球心O在线段EF上,连接OA,OC,求出半径,然后计算球的表面积.
解答 解:取AB,CD中点分别为E,F,连接EF,AF,BF,
由题意知AF⊥BF,AF=BF,如图所示;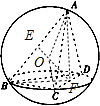
EF=$\frac{1}{2}$AB=$\sqrt{6}$,
易知三棱锥的外接球球心O在线段EF上,
连接OA,OC,有R2=AE2+OE2,R2=CF2+OF2,
∴OF2-OE2=${(\sqrt{6})}^{2}$-22=2,
∴(OE+OF)(OF-OE)=2,
∴OF-OE=$\frac{2}{\sqrt{6}}$;
又OF+OE=$\sqrt{6}$,
解得OF=$\frac{2}{3}$$\sqrt{6}$,
∴R2=22+${(\frac{2\sqrt{6}}{3})}^{2}$=$\frac{20}{3}$,
所以外接球的表面积为S=4πR2=$\frac{80π}{3}$.
故答案为:$\frac{80π}{3}$.
点评 本题主要考查了球的内接几何体的相关计算问题,也考查了空间想象能力与运算求解能力,是综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.若集合A={x|y=$\frac{1}{3-x}$+lg(x+1)},B={x|$\frac{x-2}{x}$≤0},则A∩B=( )
| A. | {x|-1≤x<2} | B. | {x|0<x≤2} | C. | {x|0≤x≤2} | D. | {x|0<x<3} |
6.在平面直角坐标系xOy中,若直线ax+y-2=0与圆心为C的圆(x-1)2+(y-a)2=16相交于A,B两点,且△ABC为直角三角形,则实数a的值是( )
| A. | -1 | B. | 0 | C. | 1 | D. | $\sqrt{2}$ |