题目内容

已知数列{log2(an-1)}(n∈N*)为等差数列,且a1=3,a3=9.

(1)求数列{an}的通项公式;

(2)证明++…+＜1.

(1)解:设等差数列{log2(an-1)}的公差为d,

    由a1=3,a3=9得2(log22+d)=log22+log28得d=1.

    所以log2(an-1)=1+(n-1)×1=n,

    即an=2n+1.

(2)证明:∵==,

    ∴++…+

   =++…+

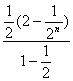==1-＜1.

练习册系列答案
相关题目
已知数列{log2（an-1）}（n∈N*）为等差数列，且a1=3，a3=9．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）证明
1
a2-a1
+
1
a3-a2
+…+
1
an+1-an
＜1．
已知数列{log2（an-1）}（n∈N*）为等差数列，且a1=3，a2=5，则
lim
n→∞
（
1
a2-a1
+
1
a3-a2
+…+
1
an+1-an
）=（　　）
A、2
B、
3
2
C、1
D、
1
2
已知数列{log2（an-1）}（n∈N*）为等差数列，且a1=3，a3=9
（1）求数列{an}的通项公式；
（2）求使
1
a2-a1
+
1
a3-a2
+…+
1
an+1-an
＞
2012
2013
成立的最小正整数n的值．
已知数列{log2(an-1)}(n∈N+)为等差数列，且a1=3，a2=5，则
1
a2-a1
+
1
a3-a2
+…+
1
an+1-an
=（　　）
（2010•抚州模拟）已知数列{log2（an-1）}（n∈N*）为等差数列，且a1=3，a2=5，则
lim
n→∞
(
1
a2-a1
+
1
a3-a2
+…+
1
an+1-an
)=
1
1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网