题目内容
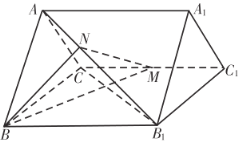
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,N为
,N为![]() 的中点.
的中点.
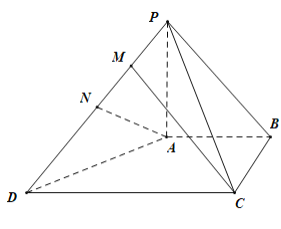
(1)求证:![]() 平面
平面![]()
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值
所成锐二面角的余弦值
(3)在线段![]() 上是否存在一点M,使得直线
上是否存在一点M,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,说明理由
的值;若不存在,说明理由
【答案】(1)见解析;(2)![]() (3)存在,
(3)存在,![]()
【解析】
(1)首先过![]() 作
作![]() ,垂足为
,垂足为![]() ,以
,以![]() 为坐标原点,分別以
为坐标原点,分別以![]() ,
,![]() ,
,![]() 为
为![]() 轴建立空间直角坐标系,分别求出
轴建立空间直角坐标系,分别求出![]() 和平面
和平面![]() 的法向量
的法向量![]() ,根据
,根据![]() 即可证明
即可证明![]() 平面
平面![]() .
.
(2)求出平面![]() 的法向量为
的法向量为![]() ,再代入二面角公式计算即可得到答案.
,再代入二面角公式计算即可得到答案.
(3)首先假设线段![]() 上存在一点
上存在一点![]() ,设
,设![]() ,
,![]() ,得到
,得到![]() ,根据直线
,根据直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求得
,求得![]() ,所以存在
,所以存在![]() ,且
,且![]() .
.
(1)过![]() 作
作![]() ,垂足为
,垂足为![]() ,则
,则![]() ,
,
以![]() 为坐标原点,分別以
为坐标原点,分別以![]() ,
,![]() ,
,![]() 为
为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
如图所示:
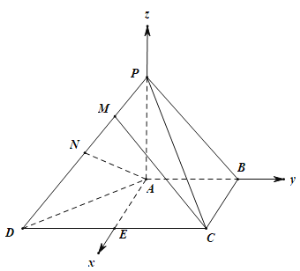
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]()
![]() ,
,![]() ,
,
则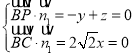 ,令
,令![]() ,解得:
,解得:![]() .
.
因为![]() ,所以
,所以![]()
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
因为![]() ,
,![]() ,
,
所以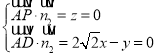 ,令
,令![]() ,解得
,解得![]() .
.
所以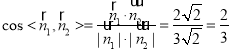 .
.
即平面![]() 与平面
与平面![]() 所成锐二面角的余弦值
所成锐二面角的余弦值![]() .
.
(3)假设线段![]() 上存在一点
上存在一点![]() ,设
,设![]() ,
,![]() ,
,![]() .
.
因为![]() ,所以
,所以![]()
则![]()
因为平面![]() 的一个法向量
的一个法向量![]()
所以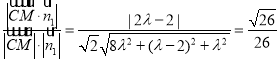 ,
,
整理得:![]() ,
,
所以![]() ,因为
,因为![]() ,所以
,所以![]() .
.
所以存在![]() ,且
,且![]() .
.

【题目】2020年寒假是特殊的寒假,因为疫情全体学生只能在家进行网上在线学习,为研究学生网上学习的情况,某校社团对男女各10名学生进行了网上在线学习的问卷调查,每名学生给出评分(满分100分),得到如图所示的茎叶图.
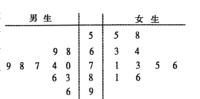
(1)根据茎叶图判断男生组和女生组哪个组对网课的评价更高?并说明理由;
(2)如图是按该20名学生的评分绘制的频率分布直方图,求![]() 的值并估计这20名学生评分的平均值(同一组中的数据用该组区间中点值作为代表);
的值并估计这20名学生评分的平均值(同一组中的数据用该组区间中点值作为代表);
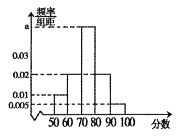
(3)求该20名学生评分的中位数![]() ,并将评分超过
,并将评分超过![]() 和不超过
和不超过![]() 的学生数填入下面的列联表:
的学生数填入下面的列联表:
超过 | 不超过 | |
男生 | ||
女生 |
根据列联表,能否有![]() 的把握认为男生和女生的评分有差异?
的把握认为男生和女生的评分有差异?
附: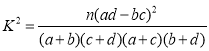 ,
,
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |