题目内容
已知函数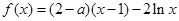 ,
,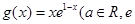 为自然对数的底数).
为自然对数的底数).
(Ⅰ)当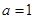 时,求
时,求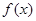 的单调区间;
的单调区间;
(Ⅱ)若函数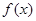 在
在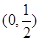 上无零点,求
上无零点,求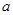 最小值;
最小值;
(Ⅲ)若对任意给定的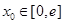 ,在
,在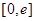 上总存在两个不同的
上总存在两个不同的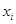
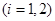 ),使
),使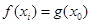 成立,求
成立,求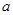 的取值范围.
的取值范围.
(Ⅰ) 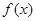 的单调递减区间为
的单调递减区间为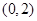 ,单调递增区间为
,单调递增区间为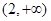 ;(Ⅱ)
;(Ⅱ) 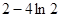 ;(Ⅲ)
;(Ⅲ) 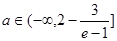 .
.
【解析】
试题分析:(Ⅰ)将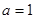 代入
代入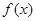 ,对
,对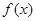 求导,令
求导,令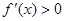 和
和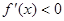 分别求出函数的单调递增区间和单调递减区间;(Ⅱ)通过分析已知先得到“对
分别求出函数的单调递增区间和单调递减区间;(Ⅱ)通过分析已知先得到“对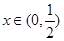 ,
,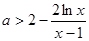 恒成立”,下面求
恒成立”,下面求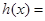
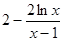 在
在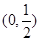 上的最大值,所以
上的最大值,所以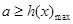 ,解出
,解出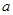 的最小值;(Ⅲ)先对
的最小值;(Ⅲ)先对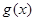 求导,判断出
求导,判断出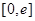 上的单调性,并求出
上的单调性,并求出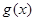 的值域,再对
的值域,再对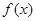 求导,确定单调性,画出简图,因为
求导,确定单调性,画出简图,因为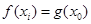 ,得到
,得到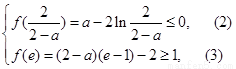 ,通过验证(2)是恒成立的,所以只需满足(3)即可,所以解出
,通过验证(2)是恒成立的,所以只需满足(3)即可,所以解出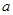 的取值范围.
的取值范围.
试题解析:(Ⅰ)当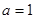 时,
时,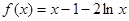 (
(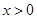 ),则
),则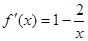 . 1分
. 1分
由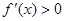 得
得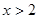 ;由
;由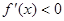 得
得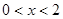 .
3分
.
3分
故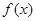 的单调递减区间为
的单调递减区间为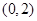 ,单调递增区间为
,单调递增区间为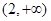 .
4分
.
4分
(Ⅱ)因为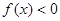 在区间
在区间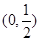 上恒成立是不可能的, 5分
上恒成立是不可能的, 5分
故要使函数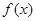 在
在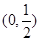 上无零点,只要对任意
上无零点,只要对任意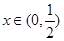 ,
, 恒成立.
恒成立.
即对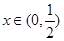 ,
,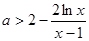 恒成立. 6分
恒成立. 6分
令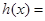
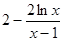 ,
,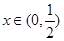 ,则
,则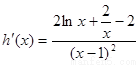 ,
,
再令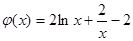 ,
,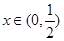 ,则
,则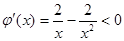 .
.
故 在
在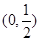 为减函数,于是
为减函数,于是
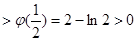 ,
,
从而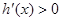 ,于是
,于是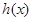 在
在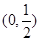 上为增函数,
上为增函数,
所以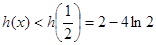 ,
8分
,
8分
故要使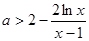 恒成立,只要
恒成立,只要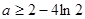 .
.
综上可知,若函数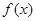 在
在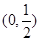 上无零点,则
上无零点,则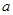 的最小值为
的最小值为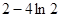 . 9分
. 9分
(Ⅲ)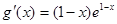 ,所以
,所以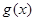 在
在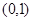 上递增,在
上递增,在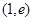 上递减.
上递减.
又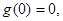
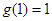 ,
,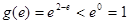 ,
,
所以函数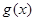 在
在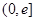 上的值域为
上的值域为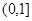 .
10分
.
10分
当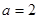 时,不合题意;
时,不合题意;
当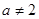 时,
时,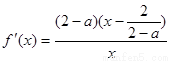 ,
,
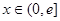 .
.
当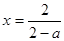 时,
时,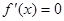 ,由题意知,
,由题意知,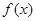 在
在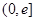 上不单调,
上不单调,
故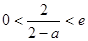 ,即
,即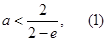 11分
11分
此时,当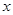 变化时,
变化时,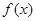 ,
,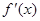 的变化情况如下:
的变化情况如下:
|
|
|
|
|
|
|
— |
0 |
+ |
|
|
↘ |
最小值 |
↗ |
又因为当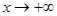 时,
时,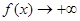 ,
,
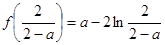 ,
,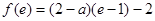 ,
,
所以,对任意给定的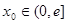 ,在
,在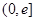 上总存在两个不同的
上总存在两个不同的 ,
,
使得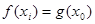 成立,当且仅当
成立,当且仅当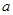 满足下列条件:
满足下列条件:
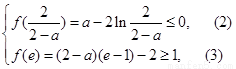 , 12分
, 12分
令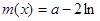
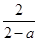 ,
,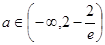 ,则
,则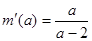 ,
,
故当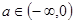 时
时 ,函数
,函数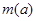 单调递增,
单调递增,
当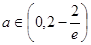 时
时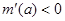 ,函数
,函数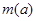 单调递减,
单调递减,
所以,对任意的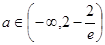 ,有
,有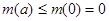 ,
,
即(2)对任意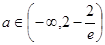 恒成立,则(3)式解得
恒成立,则(3)式解得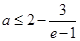 (4) . 13分
(4) . 13分
综合(1)与(4)可知,当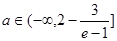 时,对任意给定的
时,对任意给定的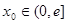 ,
,
在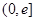 上总存在两个不同的
上总存在两个不同的 ,使得
,使得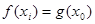 成立. 14分
成立. 14分
考点:1.用导数求函数的单调区间;2.用导数研究函数的零点;3.恒成立问题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案

 其中
其中 为自然对数的底数,
为自然对数的底数,  .
. ,求函数
,求函数 的最值;
的最值; ,都有
,都有 成立,求
成立,求 的取值范围.
的取值范围. .(
.( 为自然对数的底)
为自然对数的底) 的最小值;
的最小值; 使得
使得 对于任意的正数
对于任意的正数 恒成立?若存在,求出
恒成立?若存在,求出 .e为自然对数的底
.e为自然对数的底 时取得最小值,求
时取得最小值,求 的值;
的值; ,求函数
,求函数 在点P
在点P 处的切线方程
处的切线方程 其中
其中 为自然对数的底数
为自然对数的底数 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程; 的取值范围;
的取值范围; 时,求函数
时,求函数 的极小值。
的极小值。