题目内容
已知函数 其中
其中 为自然对数的底数,
为自然对数的底数,  .
.
(1)设 ,求函数
,求函数 的最值;
的最值;
(2)若对于任意的 ,都有
,都有 成立,求
成立,求 的取值范围.
的取值范围.
【答案】
(1)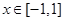 时,
时,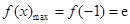 ,
,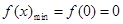 ;(2)
;(2)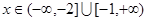
【解析】
试题分析:(1)将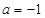 代入解析式,利用导函数求出驻点
代入解析式,利用导函数求出驻点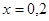 然后在
然后在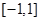 分析导函数的正负,从而得出函数的单调性求出最值
分析导函数的正负,从而得出函数的单调性求出最值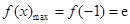 ,
,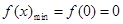 ;(2)将对于任意的
;(2)将对于任意的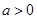 ,都有
,都有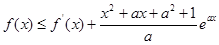 成立转化为对任意
成立转化为对任意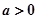 ,
,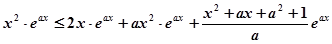 恒成立,然后利用参变分离求解即可.
恒成立,然后利用参变分离求解即可.
试题解析:(1)当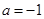 时,
时,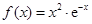 ,
,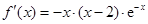 . 1分
. 1分
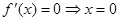 或
或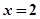 ,当
,当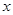 在
在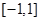 上变化时,
上变化时,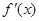 ,
,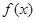 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
- |
|
+ |
|
|
|
|
|
|
|
1/e |
4分
∴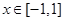 时,
时,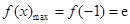 ,
,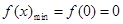 . 5分
. 5分
(2)命题等价于对任意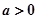 ,
,
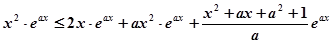 恒成立,
恒成立,
即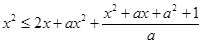 对任意
对任意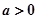 恒成立.
恒成立.
则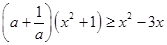 ,有
,有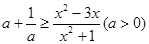 ,
,
又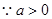
 ,
9′
,
9′
只需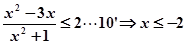 或
或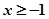 .
.
综上: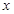 的取值范围为
的取值范围为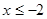 或
或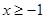 .
12′
.
12′
考点:1.利用导数处理函数的单调性和最值;2.利用导数处理不等式恒成立问题

练习册系列答案
相关题目
已知函数 其中
其中 为自然对数的底数,
为自然对数的底数,
 .(Ⅰ)设
.(Ⅰ)设 ,求函数
,求函数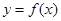 的最值;(Ⅱ)若对于任意的
的最值;(Ⅱ)若对于任意的 ,都有
,都有 成立,求
成立,求 的取值范围.
的取值范围.
【解析】第一问中,当 时,
时, ,
, .结合表格和导数的知识判定单调性和极值,进而得到最值。
.结合表格和导数的知识判定单调性和极值,进而得到最值。
第二问中,∵ ,
, ,
,
∴原不等式等价于: ,
,
即 , 亦即
, 亦即
分离参数的思想求解参数的范围
解:(Ⅰ)当 时,
时, ,
, .
.
当 在
在 上变化时,
上变化时, ,
, 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
- |
|
+ |
|
|
|
|
|
|
|
1/e |
∴ 时,
时, ,
, .
.
(Ⅱ)∵ ,
, ,
,
∴原不等式等价于: ,
,
即 , 亦即
, 亦即 .
.
∴对于任意的 ,原不等式恒成立,等价于
,原不等式恒成立,等价于 对
对 恒成立,
恒成立,
∵对于任意的 时,
时, 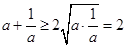 (当且仅当
(当且仅当 时取等号).
时取等号).
∴只需 ,即
,即 ,解之得
,解之得 或
或 .
.
因此, 的取值范围是
的取值范围是









 (
( 为常数,
为常数, 是自然对数的底数),曲线
是自然对数的底数),曲线 在点
在点 处的切线与
处的切线与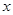 轴平行.
轴平行. 的单调区间;
的单调区间; ,其中
,其中 为
为 .
.