题目内容
(本小题共12分)已知函数![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]() (
(![]() 为常数),
为常数),![]() 是实数集
是实数集![]() 上的奇函数.(Ⅰ)求证:
上的奇函数.(Ⅰ)求证:![]() ;
;
(Ⅱ)讨论关于![]() 的方程:
的方程:![]()
![]() 的根的个数;
的根的个数;
(Ⅲ)设![]() ,证明:
,证明:![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(Ⅰ) 见解析 (Ⅱ) 见解析 (Ⅲ)见解析
解析:
(I)证:令![]() ,令
,令![]() 时
时
![]() 时,
时,![]() . ∴
. ∴![]()
∴![]() 即
即![]() .
.
(II)∵![]() 是R上的奇函数 ∴
是R上的奇函数 ∴![]() ∴
∴![]()
∴![]() ∴
∴![]() 故
故![]() .
.
故讨论方程![]() 在
在![]() 的根的个数.
的根的个数.
即![]() 在
在![]() 的根的个数.
的根的个数.![]()
令![]() .注意
.注意![]() ,方程根的个数即交点个数.
,方程根的个数即交点个数.
对![]() ,
,  ,
,
令![]() , 得
, 得![]() , 当
, 当![]() 时,
时,![]() ; 当
; 当![]() 时,
时,![]() . ∴
. ∴![]() ,
,
当![]() 时,
时,![]() ; 当
; 当![]() 时,
时,![]() , 但此时
, 但此时
![]() ,此时以
,此时以![]() 轴为渐近线。
轴为渐近线。
①当![]() 即
即![]() 时,方程无根;
时,方程无根;
②当![]() 即
即![]() 时,方程只有一个根.
时,方程只有一个根.
③当![]() 即
即![]() 时,方程有两个根.
时,方程有两个根.
(Ⅲ)由(1)知![]() , 令
, 令![]() ,
,
∴![]() ,于是
,于是![]() ,
,
∴![]()
 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 -aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间;
-aln(x+1),a∈R.(1)若a=-4,求函数f(x)的单调区间; 上任意一点P到两个定点F1(-
上任意一点P到两个定点F1(- ,0)和F2(
,0)和F2( 与曲线
与曲线 为坐标原点),求直线
为坐标原点),求直线
 的最小正周期和最小值;
的最小正周期和最小值; ,
, ,求证:
,求证: .
.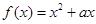 的最小值不小于
的最小值不小于 , 且
, 且 .
. 的解析式;
的解析式; 的最小值为实数
的最小值为实数 的函数
的函数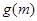 ,求函数
,求函数 ,集合
,集合
 ,求实数
,求实数 的取值范围.
的取值范围.