题目内容
15.平面内与两个定点F1,F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆,这两个定点做椭圆的焦点,两焦点的距离叫做椭圆的焦距.集合P={M|MF1|+|MF2|=2a},|F1F2|=2c,其中a>0,c>0,且a,c为常数:
(1)若a>c,则集合P为椭圆;
(2)若a=c,则集合P为线段;
(3)若a<c,则集合P为空集.
分析 (1)运用椭圆的定义,可得a>c;(2)由三角形的边角关系可得a=c;(3)运用三角形的边角关系,可得a=c.
解答 解:(1)由椭圆的定义可得,若2a>2c,P为椭圆;
(2)若集合P={M|MF1|+|MF2|=2c},即2a=2c,
P为线段;
(3)若2a<2c,即a<c,由三角形的边角关系,可得M点不存在,即P为空集.
故答案为:(1)a>c,(2)a=c,(3)a<c.
点评 本题考查椭圆的定义的理解,注意a,c的大小比较,以及三角形的边角关系,属于基础题和易错题.

练习册系列答案
相关题目
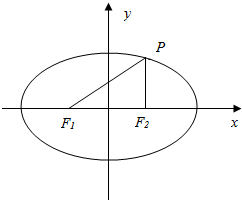 如图,$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上任一点,F1,F2为椭圆的左、右焦点,求|PF1|的 最大值和最小值.
如图,$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上任一点,F1,F2为椭圆的左、右焦点,求|PF1|的 最大值和最小值.