题目内容
4.已知定义在R上的偶函数f(x)在(0,+∞)上为增函数,且f($\frac{1}{3}$)=0,求使不等式f(x+1)>0成立的x的取值范围.分析 利用偶函数的图象关于y轴对称,又且在[0,+∞)上为增函数,将不等式中的抽象法则f脱去,解绝对值不等式求出x的取值范围.
解答 解:∵f(x)是定义在R上的偶函数,f($\frac{1}{3}$)=0,且在[0,+∞)上为增函数
∴不等式f(x+1)>0可化为|x+1|>$\frac{1}{3}$
∴解得x>-$\frac{2}{3}$或x<-$\frac{4}{3}$.
点评 本题考查利用函数的对称性及函数的单调性脱抽象的法则,将抽象不等式转化为具体不等式解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
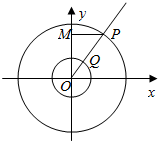 如图所示,以原点O为圆心的两个同心圆的半径分别为3和1,过原点O的射线交大圆于点P,交小圆于点Q,P在y轴上的射影为M,动点N满足$\overrightarrow{PM}$=λ$\overrightarrow{PN}$且$\overrightarrow{PM}$•$\overrightarrow{QN}$=0.
如图所示,以原点O为圆心的两个同心圆的半径分别为3和1,过原点O的射线交大圆于点P,交小圆于点Q,P在y轴上的射影为M,动点N满足$\overrightarrow{PM}$=λ$\overrightarrow{PN}$且$\overrightarrow{PM}$•$\overrightarrow{QN}$=0.