题目内容
已知函数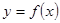 对于任意正实数
对于任意正实数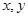 都有
都有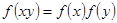 ,且
,且 时,
时,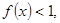
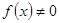 。
。
(1)证明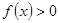
(2)求证: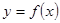 在
在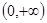 上为减函数。
上为减函数。
【答案】
(1)先证明 ,再用反证法证明
,再用反证法证明 (2)用单调性定义,设出
(2)用单调性定义,设出 ,得
,得 ,从而得证.
,从而得证.
【解析】
试题分析:(1)由题意可知, ,
,
假设 ,使
,使 则对
则对 与题设矛盾,
与题设矛盾,
故对 。
。
(2)设 则
则 由已知
由已知
 在
在 上递减。
上递减。
考点:本小题主要考查抽象函数的性质及证明,考查学生的推理论证能力.
点评:抽象函数问题,关键是“赋值法”,而要证明单调性,对于抽象函数来说,只能紧扣单调性的定义.

练习册系列答案
相关题目
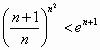 都成立.
都成立.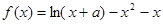 在点
在点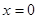 处取得极值。
处取得极值。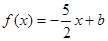 在区间[0,2]上有两个不等实根,求b的取值范围;
在区间[0,2]上有两个不等实根,求b的取值范围;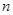 ,不等式
,不等式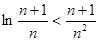 。
。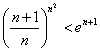 都成立.
都成立.