题目内容

已知向量
p
=(2，-3)，
q
=(x，6)，且
p
∥
q
，则
p
+
q
的值为
（-2，3）．
（-2，3）．
．
分析：根据给出的两个向量
p
和
q
的坐标，利用两个向量共线的坐标表示求出x的值，然后直接运用向量的坐标加法进行计算．
解答：解：由向量
p
=(2，-3)，
q
=(x，6)，且
p
∥
q
，
得：2×6-（-3）•x=0，所以，x=-4．
所以，
q
=(-4，6)，
则
p
+
q
=（2，-3）+（-4，6）
=（（2-4），（-3+6））
=（-2，3）．
故答案为（-2，3）．
点评：本题考查了平行向量和共线向量，考查了平面向量的坐标运算，向量
a
=(x1，y1)，
b
=(x2，y2)，则
a
∥
b
?x1y2-x2y1=0，此题是基础题．
练习册系列答案
相关题目
已知向量
p
=(x，a-3)，
q
=(x，x+a)，f(x)=
p
•
q
．
（Ⅰ）若方程f（x）=0在区间（1，+∞）上有两实根，求实数a的取值范围；
（Ⅱ）设实数m、n、r满足：m、n、r中的某一个数恰好等于a，且另两个恰为方程f（x）=0的两实根，判断①m+n+r，②m2+n2+r2，③m3+n3+r3是否为定值？若是定值请求出；若不是定值，请把不是定值的表示为函数g（a），并求g（a）的最小值；
（Ⅲ）给定函数h（x）=bx+1（b＞0），若对任意的x0∈[2，3]，总存在x1∈[1，2]，使得g（x0）=h（x1），求实数b的取值范围．
已知向量
p
=(2cosωx+2sinωx，f(x))，
q
=(1，cosωx)，ω＞0且
p
∥
q
，函数f（x）图象上相邻两条对称轴之间的距离是2π．
（Ⅰ）求函数f（x）的单调递减区间；
（Ⅱ）设函数g（x）=f（x+φ），φ∈（0，π），若g（x）为偶函数，求g（x）的最大值及相应的x值．
已知向量
p
=（cos2x，a），
q
=（a，2+
3
sin2x），函数f（x）=
p
•
q
-5（a∈R，a≠0）
（1）求函数f(x)在[0，
π
2
]上的最大值
（2）当a=2时，若对任意的t∈R，函数y=f（x），x∈（t，t+b]的图象与直线y=-1有且仅有两个不同的交点，试确定b的值，（不必证明），并求函数y=f（x）在（0，b]上的单调递增区间．
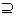已知向量p=(2，x-1)，q=(x，-3)，且p⊥q，若由x的值构成的集合A满足A{x|ax=2}，则实数a构成的集合是

[     ]

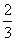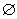
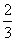A．{0}
B．{}
C．
D．{0，}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网