题目内容
20.积分${∫}_{3}^{4}$lnxdx和${∫}_{3}^{4}$ln2xdx的大小关系是${∫}_{3}^{4}$lnxdx<${∫}_{3}^{4}$ln2xdx.分析 先构造函数f(x)=lnx,g(x)=ln2x,由于当x∈[3,4]时,有f(x)<g(x)在x∈[3,4]恒成立,所以可以得出${∫}_{3}^{4}$lnxdx<${∫}_{3}^{4}$ln2xdx.
解答 解:设f(x)=lnx,g(x)=ln2x,
当x∈[3,4]时,lnx≥ln3>lne=1,
因此,ln2x>lnx在x∈[3,4]恒成立,
即f(x)<g(x)在x∈[3,4]恒成立,
根据定积分的以及意义可知,
${∫}_{3}^{4}$f(x)dx<${∫}_{3}^{4}$g(x)dx,
即${∫}_{3}^{4}$lnxdx<${∫}_{3}^{4}$ln2xdx,
故答案为:${∫}_{3}^{4}$lnxdx<${∫}_{3}^{4}$ln2xdx.
点评 本题主要考查了定积分及其运算,涉及定积分的几何意义和大小关系的比较,属于中档题.

练习册系列答案
相关题目
10.已知函数f (x)是定义在实数集R上不恒为零的偶函数,且f (-1)=0,若对任意的实数x都有xf (x+1)=(1+x) f (x)成立,则$\sum_{k-0}^{2010}f(\frac{k}{2})$ 的值是( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{5}{2}$ |
11.定义在R上的偶函数f(x)满足:对任意的x1,x2∈[0,+∞)(x1≠x2),有$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$<0.则( )
| A. | $f({0.7^6})<f({log_{0.7}}6)<f({6^{0.5}})$ | B. | f(0.76)<f(60.5)<f(log0.76) | ||
| C. | $f({log_{0.7}}6)<f({0.7^6})<f({6^{0.5}})$ | D. | $f({log_{0.7}}6)<f({6^{0.5}})<f({0.7^6})$ |
12.AB是圆O的直径,点C,D在圆上,且AB=4,∠AOC=∠A0D=120°,点E,F分别在线段上,且$\overrightarrow{OE}$=λ$\overrightarrow{OC}$,$\overrightarrow{OF}$=2λ$\overrightarrow{OD}$,则$\overrightarrow{AE}$•$\overrightarrow{BF}$的最大值为( )
| A. | -$\frac{1}{4}$ | B. | $\frac{1}{4}$ | C. | -$\frac{15}{4}$ | D. | $\frac{15}{4}$ |
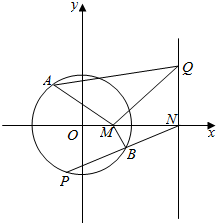 如图,自点M(1,0)引直线交椭圆$\frac{{x}^{2}}{4}$+y2=1于A,B两点,直线l:x=4与x轴交于点N,设点A关于x轴的对称点为P(异于点B).
如图,自点M(1,0)引直线交椭圆$\frac{{x}^{2}}{4}$+y2=1于A,B两点,直线l:x=4与x轴交于点N,设点A关于x轴的对称点为P(异于点B).