题目内容
设集合A={x|x2+2x-3>0},B={x|x2-2ax-1≤0,a>0}.若A∩B中恰含有一个整数,求实数a的取值范围.
解 A={x|x2+2x-3>0}={x|x>1或x<-3},
函数y=f(x)=x2-2ax-1的对称轴为x=a>0,
f(-3)=6a+8>0,
根据对称性可知,要使A∩B中恰含有一个整数,则这个整数解为2,所以有f(2)≤0且f(3)>0,
 即
即 ≤a<
≤a< .
.
故实数a的取值范围为

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则直线
,则直线 被圆
被圆 所截得的弦长为( ) A.
所截得的弦长为( ) A. B.1 C.
B.1 C. D
D .
.
 关于直线
关于直线 对称的直线方程是( )
对称的直线方程是( ) B.
B. C.
C. D.
D.
 ,集合B={y|y=x2,x∈A},则A∩B=( )
,集合B={y|y=x2,x∈A},则A∩B=( ) B.{2}
B.{2} ,如果p是q的充分不必要条件,那么k的取值范围是( )
,如果p是q的充分不必要条件,那么k的取值范围是( )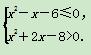
 -
-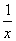 (a>0,x>0),若f(x)在
(a>0,x>0),若f(x)在 上的值域为
上的值域为