题目内容
【题目】如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,AB=2,∠BAD=60°,M是PD的中点.

(Ⅰ)求证:OM∥平面PAB;
(Ⅱ)平面PBD⊥平面PAC;
(Ⅲ)当三棱锥C﹣PBD的体积等于 ![]() 时,求PA的长.
时,求PA的长.
【答案】(Ⅰ)见证明;(Ⅱ)见证明(Ⅲ)![]()
【解析】
(Ⅰ)先证明OM∥PB,再证明OM∥平面PAB; (Ⅱ)先证明BD⊥平面PAC,再证明平面PBD⊥平面PAC;(Ⅲ)根据![]() 求出PA的长.
求出PA的长.
(Ⅰ)
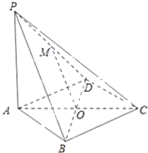
证明:在△PBD中,因为O,M分别是BD,PD的中点,
所以OM∥PB.又OM 平面PAB, PB平面PAB,
所以OM∥平面PAB.
(Ⅱ)因为底面ABCD是菱形,所以BD⊥AC.
因为PA⊥平面ABCD,BD平面ABCD,
所以PA⊥BD.又AC∩PA=A,
所以BD⊥平面PAC.
又BD平面PBD,
所以平面PBD⊥平面PAC.
(Ⅲ)因为底面ABCD是菱形,且AB=2,∠BAD=60°,
所以![]()
又![]() ,三棱锥
,三棱锥![]() 的高为PA,
的高为PA,
所以![]() ,解得
,解得![]() .
.

练习册系列答案
相关题目