题目内容
“若 ,则
,则 是函数
是函数 的极值点,因为
的极值点,因为 中,
中,  且
且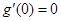 ,所以0是
,所以0是 的极值点.”在此“三段论”中,下列说法正确的是( )
的极值点.”在此“三段论”中,下列说法正确的是( )
| A.推理过程错误 | B.大前提错误 | C.小前提错误 | D.大、小前提错误 |
B
解析试题分析:极值点的第一充分条件:设函数 在
在 的一个邻域内可微(在
的一个邻域内可微(在 处可以不可微,但必须连续),若当
处可以不可微,但必须连续),若当 在该邻域内由小于
在该邻域内由小于 连续地变为大于
连续地变为大于 时,其导数
时,其导数 改变符号,则
改变符号,则 为函数的极值点;
为函数的极值点;
极值点的第二充分条件:设函数 在
在 处的二阶导数存在,若
处的二阶导数存在,若 ,且
,且 ,则
,则 为函数的极值点;所以本题当中的大前提错误的,所以选B。
为函数的极值点;所以本题当中的大前提错误的,所以选B。
考点:演绎推理、函数极值的定义

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
把正整数按一定的规则排成了如图所示的三角形数表.设 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第 行,从左往右数第
行,从左往右数第 个数,若
个数,若 ,则
,则 与
与 的和为( )
的和为( )
| A.105 | B.103 | C.82 | D.81 |
将正偶数按下表排成4列:
则2 004在 ( ).
| A.第251行,第1列 | B.第251行,第2列 |
| C.第250行,第2列 | D.第250行,第4列 |
用数学归纳法证明“ 时,从“
时,从“ 到
到 ”时,左边应增添的式子是( )
”时,左边应增添的式子是( )
A. | B. | C. | D. |
对于任意正整数n,定义“ ”如下:
”如下:
当n是偶数时, ,
,
当n是奇数时,
现在有如下四个命题:
① ;
;
② ;
;
③ 的个位数是0;
的个位数是0;
④ 的个位数是5。
的个位数是5。
其中正确的命题有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
用反证法证明命题:“若整系数一元二次方程 有有理根,那么
有有理根,那么 中至少有一个是偶数时,下列假设中正确的是
中至少有一个是偶数时,下列假设中正确的是
A.假设 都是偶数 都是偶数 |
B.假设 都不是偶数 都不是偶数 |
C.假设 至多有一个是偶数 至多有一个是偶数 |
D.假设 至多有两个是偶数 至多有两个是偶数 |
 为8时,则其输出的结果是 .
为8时,则其输出的结果是 .
 和S=
和S= ,求数列{an}的通项公式.
,求数列{an}的通项公式.
 、
、 、
、 、
、 号位上(如图),第一次前后
号位上(如图),第一次前后 这样交替进行下去,那么第
这样交替进行下去,那么第 次互换座位后,小兔坐
次互换座位后,小兔坐