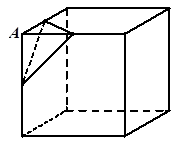题目内容
如图,三棱柱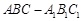 中,侧面
中,侧面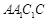
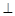 底面
底面 ,
,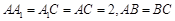 ,且
,且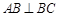 ,O为
,O为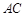 中点.
中点.
(Ⅰ)证明: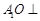 平面
平面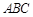 ;
;
(Ⅱ)求直线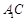 与平面
与平面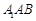 所成角的正弦值
所成角的正弦值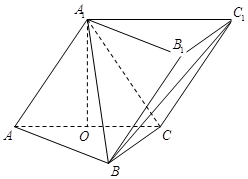
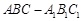 中,侧面
中,侧面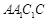
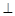 底面
底面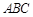 ,
,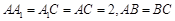 ,且
,且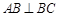 ,O为
,O为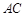 中点.
中点.(Ⅰ)证明:
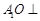 平面
平面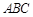 ;
;(Ⅱ)求直线
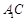 与平面
与平面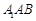 所成角的正弦值
所成角的正弦值
(Ⅰ)证明略(Ⅱ) .
.
 .
.Ⅰ)先证明 ,根据平面
,根据平面 平面
平面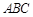 ,证得
,证得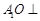 平面
平面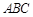 ;(Ⅱ)向量法求解。
;(Ⅱ)向量法求解。
解:(Ⅰ)证明:因为 ,且O为AC的中点,所以
,且O为AC的中点,所以 . ………1分
. ………1分
又由题意可知,平面 平面
平面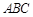 ,交线为
,交线为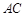 ,且
,且 平面
平面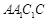 ,所以
,所以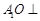 平面
平面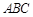 . ………4分
. ………4分
(Ⅱ)如图,以O为原点, 所在直线分别为x,y,z轴建立空间直角坐标系.
所在直线分别为x,y,z轴建立空间直角坐标系.

由题意可知, 又
又

所以得:
则有: ………6分
………6分
设平面 的一个法向量为
的一个法向量为 ,则有
,则有
 ,令
,令 ,得
,得
所以 . ………………7分
. ………………7分
 . ………………9分
. ………………9分
因为直线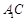 与平面
与平面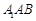 所成角
所成角 和向量
和向量 与
与 所成锐角互余,所以
所成锐角互余,所以 .
.
 ,根据平面
,根据平面 平面
平面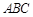 ,证得
,证得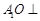 平面
平面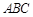 ;(Ⅱ)向量法求解。
;(Ⅱ)向量法求解。解:(Ⅰ)证明:因为
 ,且O为AC的中点,所以
,且O为AC的中点,所以 . ………1分
. ………1分又由题意可知,平面
 平面
平面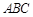 ,交线为
,交线为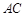 ,且
,且 平面
平面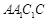 ,所以
,所以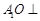 平面
平面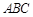 . ………4分
. ………4分(Ⅱ)如图,以O为原点,
 所在直线分别为x,y,z轴建立空间直角坐标系.
所在直线分别为x,y,z轴建立空间直角坐标系.
由题意可知,
 又
又

所以得:

则有:
 ………6分
………6分 设平面
 的一个法向量为
的一个法向量为 ,则有
,则有 ,令
,令 ,得
,得
所以
 . ………………7分
. ………………7分 . ………………9分
. ………………9分因为直线
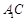 与平面
与平面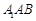 所成角
所成角 和向量
和向量 与
与 所成锐角互余,所以
所成锐角互余,所以 .
.
练习册系列答案
相关题目










 ,那么,动点N在平面ABCD内的轨迹是( )
,那么,动点N在平面ABCD内的轨迹是( )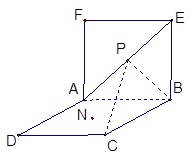
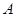 是棱长为
是棱长为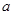 的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:①有
的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:①有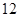 个顶点;②有
个顶点;②有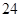 条棱;③有
条棱;③有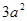 ;⑤体积为
;⑤体积为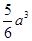 .其中正确的结论是____________.(要求填上所有正确结论的序号)
.其中正确的结论是____________.(要求填上所有正确结论的序号)