题目内容
已知抛物线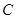 的顶在坐标原点,焦点
的顶在坐标原点,焦点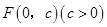 到直线
到直线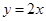 的距离是
的距离是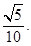
(1)求抛物线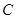 的方程;
的方程;
(2)若直线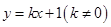 与抛物线
与抛物线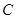 交于
交于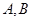 两点,设线段
两点,设线段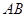 的中垂线与
的中垂线与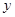 轴交于点
轴交于点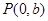 ,求
,求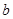 的取值范围.
的取值范围.
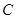 的顶在坐标原点,焦点
的顶在坐标原点,焦点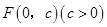 到直线
到直线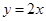 的距离是
的距离是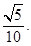
(1)求抛物线
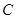 的方程;
的方程;(2)若直线
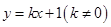 与抛物线
与抛物线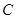 交于
交于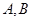 两点,设线段
两点,设线段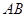 的中垂线与
的中垂线与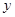 轴交于点
轴交于点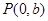 ,求
,求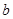 的取值范围.
的取值范围.(1) (2)
(2)
 (2)
(2)
试题分析:(1)已知点
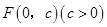 到直线
到直线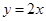 的距离利用距离公式
的距离利用距离公式 可求得
可求得 ,可直接写出抛物线方程; (2)把直线方程与抛物线方程联立整理成二次方程
,可直接写出抛物线方程; (2)把直线方程与抛物线方程联立整理成二次方程 ,用韦达定理可求出线段
,用韦达定理可求出线段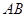 中点的坐标
中点的坐标 ,再写出中垂线方程
,再写出中垂线方程 ,即可求出直线与
,即可求出直线与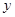 轴交点的纵坐标
轴交点的纵坐标 ,利用二次函数求值域的方法可求出
,利用二次函数求值域的方法可求出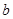 的范围.这个过程中不用讨论判别式,不用讨论斜率,值域也是二次函数的值域问题,是直线与圆锥曲线中的较易者.
的范围.这个过程中不用讨论判别式,不用讨论斜率,值域也是二次函数的值域问题,是直线与圆锥曲线中的较易者.试题解析:(1)由题意,
 ,故
,故
所以抛物线
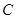 的方程为
的方程为 .
.(2)设
 ,则由
,则由 得
得 ,
,则
 ,所以线段
,所以线段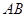 的中点坐标为
的中点坐标为 ,
,线段
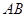 的中垂线方程为
的中垂线方程为 ,
,即
 ,令
,令 ,则
,则 ,
,所以
 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
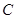 经过
经过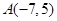 、
、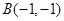 两点
两点 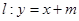 交双曲线
交双曲线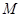 、
、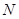 两点,且线段
两点,且线段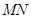 被圆
被圆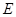 :
: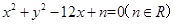 三等分,求实数
三等分,求实数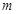 、
、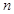 的值
的值 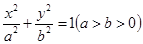 的左、右焦点和短轴的一个端点构成边长为4的正三角形.
的左、右焦点和短轴的一个端点构成边长为4的正三角形.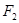 的直线
的直线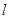 与椭圆C相交于A、B两点,若
与椭圆C相交于A、B两点,若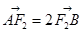 ,求直线
,求直线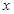 轴的抛物线经过点
轴的抛物线经过点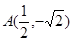 .
.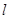 过定点
过定点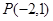 ,斜率为
,斜率为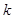 ,当
,当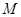 :
: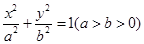 经过点
经过点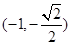 ,
,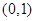 .
.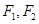 ,过点
,过点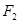 的直线交椭圆
的直线交椭圆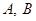 两点,求
两点,求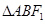 面积的最大值.
面积的最大值. 在抛物线
在抛物线 :
: 上.
上. 的三个顶点都在抛物线
的三个顶点都在抛物线 ,
, ,
, 所在直线的斜率分别为
所在直线的斜率分别为 ,
, ,
, ,求
,求 的值;
的值; 的四个顶点都在抛物线
的四个顶点都在抛物线 ,
, 所在直线的斜率分别为
所在直线的斜率分别为 ,求
,求 的值.
的值. 、
、 为椭圆
为椭圆 的左、右焦点,且点
的左、右焦点,且点 在椭圆
在椭圆 的直线
的直线 交椭圆
交椭圆 两点,则
两点,则 的内切圆的面积是否存在最大值?
的内切圆的面积是否存在最大值?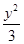 =1.
=1.
 且和抛物线
且和抛物线 相切的直线
相切的直线 方程为 .
方程为 .