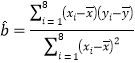题目内容
【题目】已知抛物线
的焦点为F，准线为l，过F的直线与E交于A，B两点，C，D分别为A，B在l上的射影，且
，M为AB中点，则下列结论正确的是（ ）
A.
B.
为等腰直角三角形
C.直线AB的斜率为
D.
的面积为4
【答案】AC
【解析】
A．根据抛物线性质，结合角度之间的关系，求解出
的度数；B．利用抛物线的焦半径结合
，判断
为等腰直角三角形的可能性；C．根据，设出直线方程完成直线
斜率的求解；D．取直线的方程，联立抛物线方程求解出
的值，根据
求解出三角形面积.
过点
向准线
作垂线，垂足为
，
，设
，
如下图所示：
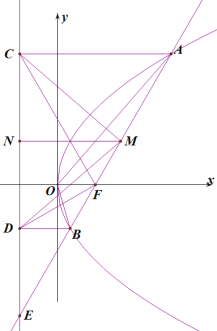
A．因为
，所以
，
又因为
，所以
，所以
平分
，
同理可知
平分
，所以
，故结论正确；
B．假设为等腰直角三角形，所以
，
所以
四点共圆且圆的半径为
，
又因为
，所以
，
所以
，所以
，所以
，显然不成立，故结论错误；
C．设直线的方程为
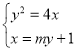，所以
，所以
，所以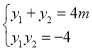
，
又因为，所以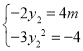
，所以
，
所以
，所以
，所以直线的斜率为
，故结论正确；
D．取
，由上可知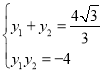
，所以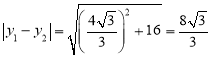
，
所以
，故结论错误.
故选：AC.
练习册系列答案
中考解读考点精练系列答案
相关题目
