题目内容
．已知圆
的方程为
，直线
的方程为
，点
在直线上，过点作圆的切线
，切点为
．
（1）若
，试求点的坐标；
（2）若
点的坐标为
，过作直线与圆交于
两点，当时，求直线
的方程；
（3）求证：经过
三点的圆必过定点，并求出所有定点的坐标.
解：（1）设
，由题可知
，所以
，解之得：
故所求点
的坐标为
或
． …………………………………………4分
（2）设直线
的方程为：
，易知
存在，由题知圆心
到直线的距离为
，所以
， …………………………………………6分
解得，
或
，ks.5u
故所求直线的方程为：
或
．………………………8分
（3）设，
的中点
，因为
是圆
的切线
所以经过
三点的圆是以
为圆心，以
为半径的圆，
故其方程为：
……………………………10分
化简得：
，此式是关于
的恒等式，
故
解得
或
所以经过三点的圆必过定点
或
.…………………………………14分
练习册系列答案
仁爱英语同步练习册系列答案
学习实践园地系列答案
相关题目
如图所示，一隧道内设双行线公路，其截面由一段圆弧和一个长方形构成．已知隧道总宽度AD为
，圆心在直线y=2x上，圆被直x－y=0截得的弦长为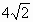
，求圆的方程．
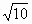，圆心在直线y=2x上，圆被直x－y=0截得的弦长为
，求圆的方程．
的离心率为
，直线
:
与以原点为圆心、以椭圆
的短半轴长为半径的圆相切.
，右焦点
，直线
过点
垂
，线段
垂直平分线交
，求点
的方程；
轴上时，在曲线
的离心率为
，
与以原点为圆心、以椭圆
的短半轴长为半径的圆相切。
过点F1，且垂直于椭圆的长轴，动直
垂直