题目内容
已知双曲线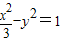 的左右焦点分别为F1F2,过F1且倾斜角为60°的直线l与双曲线交于M,N两点,则△MNF2的内切圆半径为 .
的左右焦点分别为F1F2,过F1且倾斜角为60°的直线l与双曲线交于M,N两点,则△MNF2的内切圆半径为 .
【答案】分析:依题意可求得直线MN的方程,与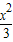 -y2=1联立,可求得|MN|,再利用双曲线的定义可求得△MNF2的周长,设F2到直线MN的距离为d,利用△MNF2的面积公式即可求得△MNF2的内切圆半径.
-y2=1联立,可求得|MN|,再利用双曲线的定义可求得△MNF2的周长,设F2到直线MN的距离为d,利用△MNF2的面积公式即可求得△MNF2的内切圆半径.
解答:解:∵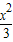 -y2=1的右焦点为F2(2,0),左焦点为F1(-2,0),
-y2=1的右焦点为F2(2,0),左焦点为F1(-2,0),
∴过F1且倾斜角为60°的直线l方程为:y=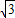 (x+2),
(x+2),
∴由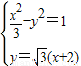 消去y得:8x2+36x+39=0,
消去y得:8x2+36x+39=0,
设M(x1,y1),N(x2,y2),
则x1,x2是方程8x2+36x+39=0的两根.
∴x1+x2=- ,x1x2=
,x1x2=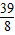 ,
,
∴|MN|=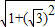 •
•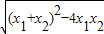
=2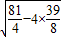 =
=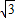 .
.
∵|MF2|-|MF1|=2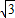 ,
,
|NF2|-|NF1|=2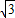 ,
,
∴|MF2|+|NF2|=4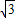 +|MN|=5
+|MN|=5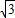 .
.
∴△MNF2的周长为|MF2|+|NF2|+|MN|=6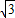 ;
;
设F2(2,0)到直线MN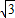 x-y+2
x-y+2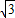 =0的距离为d,
=0的距离为d,
则d=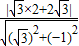 =2
=2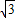 ,
,
∴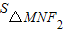 =
= |MN|•d=
|MN|•d= ×
×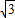 ×2
×2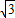 =3.
=3.
设△MNF2的内切圆半径为r,
则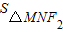 =
= (|MF2|+|NF2|+|MN|)•r=3
(|MF2|+|NF2|+|MN|)•r=3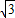 r,
r,
∴3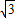 r=3,
r=3,
∴r=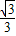 .
.
故答案为: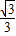 .
.
点评:本题考查直线与圆锥曲线的相交,考查点到直线间的距离公式,考查转化与运算的综合应用,属于难题.
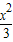 -y2=1联立,可求得|MN|,再利用双曲线的定义可求得△MNF2的周长,设F2到直线MN的距离为d,利用△MNF2的面积公式即可求得△MNF2的内切圆半径.
-y2=1联立,可求得|MN|,再利用双曲线的定义可求得△MNF2的周长,设F2到直线MN的距离为d,利用△MNF2的面积公式即可求得△MNF2的内切圆半径.解答:解:∵
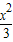 -y2=1的右焦点为F2(2,0),左焦点为F1(-2,0),
-y2=1的右焦点为F2(2,0),左焦点为F1(-2,0),∴过F1且倾斜角为60°的直线l方程为:y=
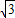 (x+2),
(x+2),∴由
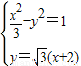 消去y得:8x2+36x+39=0,
消去y得:8x2+36x+39=0,设M(x1,y1),N(x2,y2),
则x1,x2是方程8x2+36x+39=0的两根.
∴x1+x2=-
 ,x1x2=
,x1x2=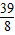 ,
,∴|MN|=
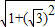 •
•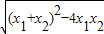
=2
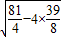 =
=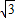 .
.∵|MF2|-|MF1|=2
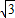 ,
,|NF2|-|NF1|=2
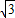 ,
,∴|MF2|+|NF2|=4
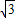 +|MN|=5
+|MN|=5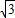 .
.∴△MNF2的周长为|MF2|+|NF2|+|MN|=6
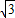 ;
;设F2(2,0)到直线MN
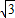 x-y+2
x-y+2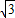 =0的距离为d,
=0的距离为d,则d=
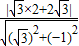 =2
=2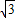 ,
,∴
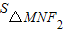 =
= |MN|•d=
|MN|•d= ×
×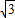 ×2
×2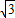 =3.
=3.设△MNF2的内切圆半径为r,
则
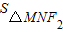 =
= (|MF2|+|NF2|+|MN|)•r=3
(|MF2|+|NF2|+|MN|)•r=3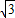 r,
r,∴3
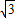 r=3,
r=3,∴r=
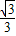 .
.故答案为:
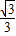 .
.点评:本题考查直线与圆锥曲线的相交,考查点到直线间的距离公式,考查转化与运算的综合应用,属于难题.

练习册系列答案
相关题目
 的左右焦点为
的左右焦点为 ,P为双曲线右支上
,P为双曲线右支上 的最小值为8a,则双曲线的离心率的取值范围是 。
的最小值为8a,则双曲线的离心率的取值范围是 。 的左右焦点分别为
的左右焦点分别为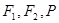 为左支上一点,若
为左支上一点,若 的最小值为
的最小值为 ,则双曲线离心率
,则双曲线离心率 的取值范围为(
)
的取值范围为(
)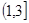 B、
B、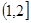 C、
C、 D、
D、
 的左右焦点分别是
的左右焦点分别是 ,
, 点是双曲线右支上一点,且
点是双曲线右支上一点,且 ,则三角形
,则三角形 的面积等于
的面积等于